【题目】在学习“二元一次方程组的解”时,数学张老师设计了一个数学活动,有A、B两组卡片,每组各三张,A组卡片上分别写有0,1,2;B组卡片上分别写有-3,-1,1。每张卡片除正面写有不同数字外,其余均相同。甲从A组随机抽取一张记为x,乙从B组随机抽取一张记为y。
(1)若甲抽出的数字是2,乙抽出的数字是-1,它们恰好是方程ax-y=5的解,求a的值;
(2)求甲、乙随机抽取一次的数恰好是方程ax-y=3的解得概率(请用树状图或列表法求解
参考答案:
【答案】(1)2;(2)![]()
【解析】试题分析:
(1)把x,y的值代入到方程ax-y=5中求解;
(2)用列表法列出所有的组合,从中找出是方程ax-y=3的解的组合的个数,再根据概率的定义求解.
试题解析:
解:(1)将x=2,y=-1代入方程得:2a+1=5,即a=2;
(2)列表得:
0 | 1 | 2 | |
-3 | (0,-3) | (1,-3) | (2,-3) |
-1 | (0,-1) | (1,-1) | (2,-1) |
1 | (0,1) | (1,1) | (2,1) |
所有等可能的情况有9种,其中(x,y)恰好为方程2x-y=3的解的情况有(0,-3),(1,-1),(2,-1)共3种情况,则P=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.

-
科目: 来源: 题型:
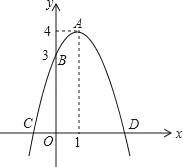
查看答案和解析>>【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用火柴棍摆成边长分别是1、2、3根火柴棍时的正方形,当边长为n根火柴棍时,若摆出的正方形所用的火柴棍的根数为S,则S= (用含n的代数式表示,n为正整数).

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中:①-22与(-2)2; ②(-3)2与-33; ③-(-32)与-32 ;④02019与02018;⑤(-1)2019与-(-1)2.其中结果相等的数据共有( )
A.1对B.2对C.3对D.4对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,以B、P、Q三点为顶底的三角形是等腰三角形?
(3)当线段PQ与线段AB相交于点O,且2AO=OB时,求∠BQP的正切值;
(4)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某海船以
 海里/小时的速度向北偏东70°方向行驶,在A处看见灯塔B在海船的北偏东40°方向,5小时后船行驶到C处,发现此时灯塔B在海船的北偏西65°方向,求此时灯塔B到C处的距离。
海里/小时的速度向北偏东70°方向行驶,在A处看见灯塔B在海船的北偏东40°方向,5小时后船行驶到C处,发现此时灯塔B在海船的北偏西65°方向,求此时灯塔B到C处的距离。
相关试题

