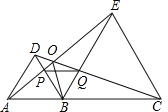
【题目】如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是 (填写序号).

参考答案:
【答案】①③④.
【解析】
试题分析:易证△ABE≌△DBC,则有∠BAE=∠BDC,从而可证到△ABP≌△DBQ,则有AP=DQ,BP=BQ,由∠PBQ=60°可得△BPQ是等边三角形,则有PQ=PB.∠BPQ=60°,从而可得∠EPB>∠EBP,即可得到EB>EP,即EC>EP,由△ABE≌△DBC可得S△ABE=S△DBC,AE=DC,从而可得点B到AE、DC的距离相等,因而点B在∠AOC的角平分线上,即可得到∠AOB=∠BOC=∠COE=60°.
解:∵△ABD和△BCE都是等边三角形,
∴BD=BA=AD,BE=BC=EC,∠ABD=∠CBE=60°,
∵点A、B、C在同一直线上,
∴∠DBE=180°﹣60°﹣60°=60°,
∴∠ABE=∠DBC=120°.
在△ABE和△DBC中,
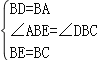 ,
,
∴△ABE≌△DBC,
∴∠BAE=∠BDC.
在△ABP和△DBQ中,
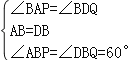 ,
,
∴△ABP≌△DBQ,
∴AP=DQ,BP=BQ.
∴①正确.
∵∠PBQ=60°,
∴△BPQ是等边三角形,
∴PQ=PB.∠BPQ=60°.
∴③正确.
∵∠EPB>∠BPQ,∠BPQ=∠EBP=60°,
∴∠EPB>∠EBP,
∴EB>EP,
∴EC>EP,
∴②不正确.
∵∠DPA=∠PDO+∠DOP,∠DPA=∠PAB+∠ABP,∠PDO=∠PAB,
∴∠DOP=∠ABP=60°,
∴∠COE=60°,∠AOC=120°.
∵△ABE≌△DBC,
∴S△ABE=S△DBC,AE=DC,
∴点B到AE、DC的距离相等,
∴点B在∠AOC的角平分线上,
∴∠AOB=∠BOC=![]() ∠AOC=60°,
∠AOC=60°,
∴∠AOB=∠BOC=∠COE=60°.
∴④正确.
故答案为①③④.
-
科目: 来源: 题型:
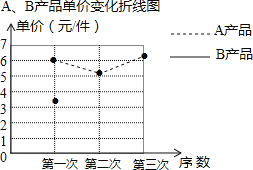
查看答案和解析>>【题目】某厂生产A、B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
并求得了A产品三次单价的平均数和方差:
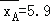 ;SA2=
;SA2= [(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]=
[(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]=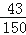
(1)补全“A、B产品单价变化的折线图”,B产品第三次的单价比上一次的单价降低了百分之多少?
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件.
则A产品这四次单价的中位数是 元/件.
若A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,则B产品的第四次单价为 元/件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则
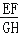 的值是( )
的值是( )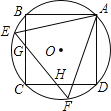
A.
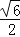 B.
B.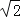 C.
C.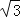 D.2
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】为解方程x4﹣5x2+4=0,我们可设x2=y,则x4=y2,原方程可化为y2﹣5y+4=0.解得y1=1,y2=4,当y=1时,x2=1,所以x=±1;当y=4时,x2=4,所以x=±2.故原方程的解为x1=1,x2=﹣1,x3=2,x4=﹣2.以上解题方法主要体现的数学思想是( )
A.数形结合 B.换元与降次 C.消元 D.公理化
-
科目: 来源: 题型:
查看答案和解析>>【题目】若将边形边数增加1条,则它的内角和增加__________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列长度的四组线段中,能组成三角形的是( )
A. 3,7,15 B. 1,2,4 C. 5,5,10 D. 2,3,3
相关试题

