【题目】△ABC为等腰直角三角形,∠ABC=90°,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角△CDE,∠DCE=90°.
(1)如图1,作EF⊥BC于F,求证:△DBC≌△CFE;
(2)在图1中,连接AE交BC于M,求![]() 的值;
的值;
(3)如图2,过点E作EH⊥CE交CB的延长线于点H,过点D作DG⊥DC,交AC于点G,连接GH.当点D在边AB上运动时,式子![]() 的值会发生变化吗?若不变,求出该值;若变化请说明理由.
的值会发生变化吗?若不变,求出该值;若变化请说明理由.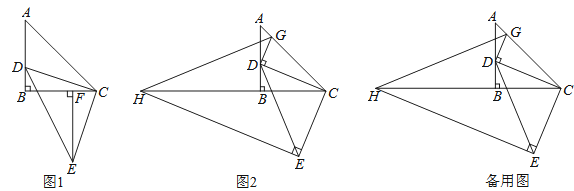
参考答案:
【答案】(1)证明:∵△CDE为等腰直角三角形,∠DCE=90°.
∴CD=CE,∠DCB+∠ECF=90°,
∵EF⊥BC,
∴∠ECF+∠CEF=90°,
∴∠DCB=∠CEF,
在△DBC和△CEF中, ,
,
∴△DBC≌△CFE;
(2)解:如图1,
∵△DBC≌△CFE,
∴BD=CF,BC=EF,
∵△ABC为等腰直角三角形,
∴AB=BC,
∴AB=EF,AD=BF,
在△ABM和△EFM中, ,
,
∴△ABM≌△EFM,
∴BM=FM,
∴BF=2BM,
∴AD=2BM,
∴![]() 的值为2;
的值为2;
(3)解:![]() 的值不变.
的值不变.
在EH上截取EQ=DG,如图2,
在△CDG和△CEQ中 ,
,
∴△CDG≌△CEQ,
∴CG=CQ,∠DCG=∠ECQ,
∵∠DCG+∠DCB=45°,
∴∠ECQ+∠DCB=45°,
而∠DCE=90°,
∴∠HCQ=45°,
∴∠HCQ=∠HCG,
在△HCG和△HCQ中, ,
,
∴△HCG≌△HCQ,
∴HG=HQ,
∴![]() =
=![]() =1.
=1.
【解析】(1)根据等腰直角三角形的性质得到CD=CE,再利用等角的余角相等得到∠DCB=∠CEF,然后根据“AAS”可证明△DBC≌△CFE;
(2)由△DBC≌△CFE得到BD=CF,BC=EF,再利用△ABC为等腰直角三角形得到AB=BC,所以AB=EF,AD=BF,接着证明△ABM≌△EFM,得到BM=FM,所以![]() =2;
=2;
(3)在EH上截取EQ=DG,如图2,先证明△CDG≌△CEQ得到CG=CQ,∠DCG=∠ECQ,由于∠DCG+∠DCB=45°,则∠ECQ+∠DCB=45°,所以∠HCQ=45°,再证明△HCG≌△HCQ,则得到HG=HQ,然后可计算出![]() =1.
=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当m+n=3时,式子m2+2mn+n2的值为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为估计全市七年级学生的体重情况,从某私立学校随机抽取20人进行调查,在这个问题中,调查的样本________(填“具有”或“不具有”)代表性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题的逆命题是假命题的是( )
A. 对顶角相等 B. 角平分线上的点到这个角的两边的距离相等
C. 如果a2=b2,那么a=b D. 同旁内角互补,两直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x+3)2﹣4的对称轴为( )
A. 直线x=3B. 直线x=﹣3C. 直线x=4D. 直线x=﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|x﹣2|+(y+3)2=0,那么yx的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,直L交AB、CD分别于点E、F,点M在线段EF上(点M不与E、F重合),N是直线CD上的一个动点(点N不与F重合)
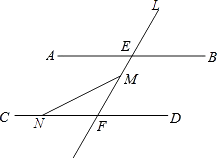
(1)当点N在射线FC上运动时(F点除外),则∠FMN+∠FNM=∠AEF,说明理由?
(2)当点N在射线FD上运动时(F点除外),∠FMN+∠FNM与∠AEF有什么关系?画出图形,猜想结论并证明.
相关试题

