【题目】如图,AB∥CD,直L交AB、CD分别于点E、F,点M在线段EF上(点M不与E、F重合),N是直线CD上的一个动点(点N不与F重合)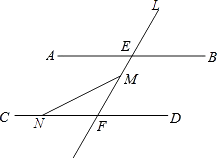
(1)当点N在射线FC上运动时(F点除外),则∠FMN+∠FNM=∠AEF,说明理由?
(2)当点N在射线FD上运动时(F点除外),∠FMN+∠FNM与∠AEF有什么关系?画出图形,猜想结论并证明.
参考答案:
【答案】
(1)
解:∵AB∥CD,
∴∠AEF+∠MFN=180°.
∵∠MFN+∠FMN+∠FNM=180°,
∴∠FMN+∠FNM=∠AEF.
(2)
解:∠FMN+∠FNM+∠AEF=180°.
理由:如图所示,
∵AB//CD,
∴∠AEF=∠MFN.
∵∠MFN+∠FMN+∠FNM=180°,
∴∠FMN+∠FNM+∠AEF=180°.
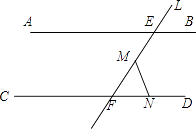
【解析】(1)利用两直线平行,同旁内角互补和三角形的内角和为180°,易得∠FMN+∠FNM=∠AEF;(2)根据两直线平行,内错角相等和三角形的内角和为180度,易得∠FMN+∠FNM+∠AEF=180°.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补).
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC为等腰直角三角形,∠ABC=90°,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角△CDE,∠DCE=90°.
(1)如图1,作EF⊥BC于F,求证:△DBC≌△CFE;
(2)在图1中,连接AE交BC于M,求 的值;
的值;
(3)如图2,过点E作EH⊥CE交CB的延长线于点H,过点D作DG⊥DC,交AC于点G,连接GH.当点D在边AB上运动时,式子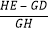 的值会发生变化吗?若不变,求出该值;若变化请说明理由.
的值会发生变化吗?若不变,求出该值;若变化请说明理由.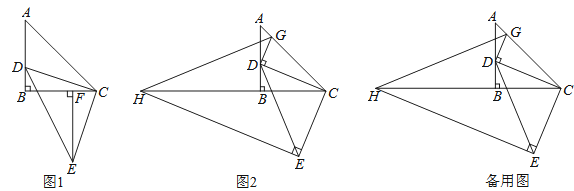
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x+3)2﹣4的对称轴为( )
A. 直线x=3B. 直线x=﹣3C. 直线x=4D. 直线x=﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|x﹣2|+(y+3)2=0,那么yx的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据:1,﹣1,3,x,4,它有唯一的众数是3,则这组数据的中位数为( )
A.﹣1
B.1
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】将一个三角形放大为与它相似的三角形,如果周长扩大为原来的3倍,那么面积扩大为原来的( )
A. 3倍B. 9倍C. 18倍D. 81倍
-
科目: 来源: 题型:
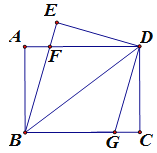
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵将折叠的图形恢复原状,点F与BC边上的点G正好重合,连接DG,若AB=6,BC=8,求DG的长.
相关试题

