【题目】如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y= ![]() 的图象相交于A(﹣2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+
的图象相交于A(﹣2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+ ![]() n=0;③S△AOP=S△BOQ;④不等式k1x+b
n=0;③S△AOP=S△BOQ;④不等式k1x+b ![]() 的解集是x<﹣2或0<x<1,其中正确的结论的序号是 .
的解集是x<﹣2或0<x<1,其中正确的结论的序号是 . 
参考答案:
【答案】②③④
【解析】解:由图象知,k1<0,k2<0,
∴k1k2>0,故①错误;
把A(﹣2,m)、B(1,n)代入y= ![]() 中得﹣2m=n,
中得﹣2m=n,
∴m+ ![]() n=0,故②正确;
n=0,故②正确;
把A(﹣2,m)、B(1,n)代入y=k1x+b得 ![]() ,
,
∴ 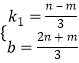 ,
,
∵﹣2m=n,
∴y=﹣mx+ ![]() m,
m,
∴P(﹣ ![]() ,0),Q(0,
,0),Q(0, ![]() m),
m),
∴OP= ![]() ,OQ=
,OQ= ![]() m,
m,
∴S△AOP= ![]() ×
× ![]() m,S△BOQ=
m,S△BOQ= ![]()
![]() m×1,
m×1,
∴S△AOP=S△BOQ;故③正确;
由图象知不等式k1x+b> ![]() 的解集是x<﹣2或0<x<1,故④正确;
的解集是x<﹣2或0<x<1,故④正确;
所以答案是:②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论:
①⊙O的半径为 ②OD∥BE ③PB=
②OD∥BE ③PB=  ④tan∠CEP=
④tan∠CEP= 
其中正确结论有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:
①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c(a≠0)有一个根为﹣
其中正确的结论个数有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,CQ的长为( )

A.5
B.7
C.8
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=﹣
 x,点A1坐标为(﹣3,0).过点A1作x轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2 , 再过点A2作x轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3 , …,按此做法进行下去,点A2016的坐标为 .
x,点A1坐标为(﹣3,0).过点A1作x轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2 , 再过点A2作x轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3 , …,按此做法进行下去,点A2016的坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|
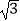 -
-  |+(
|+(  -1)0+2sin45°﹣2cos30°+(
-1)0+2sin45°﹣2cos30°+(  )﹣1 .
)﹣1 .
相关试题

