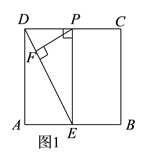
【题目】边长为2的正方形ABCD中E是AB的中点,P在射线DC上从D出发以每秒1个单位长度的速度运动,过P做PF⊥DE,当运动时间为__________秒时,以点P、F、E为顶点的三角形与△AED相似

参考答案:
【答案】1或![]()
【解析】∵四边形ABCD是正方形,PF⊥DE,
∴∠A=∠DFP=∠ADC=90°,
∴∠ADE+∠EDP=∠EDP+∠DPF=90°,
∴∠ADE=∠FPD,
∴△ADE∽△FPD.
(1)如图1,当∠DPE=90°时,易得△FPD∽△FEP,则△ADE∽△FEP,
此时四边形AEPD是矩形,
∴DP=AE=1,
∴t=1,即当t=1时,△ADE∽△FEP;
(2)如图2,当DP=EP时,易得△FPE≌△FPD,则△FEP∽△ADE,
此时四边形AEHD是矩形,
∴DH=AE=1,HP=x-1,HE=AD=2,
∴PE2=HE2+HP2=PD2,
∴![]() ,解得:
,解得: ![]() ;
;

综上所述,当![]() 或
或![]() 时,以点P、F、E为顶点的三角形与△AED相似.
时,以点P、F、E为顶点的三角形与△AED相似.
故答案为:1或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下(注:水费按月份结算):
价目表
每月用水量
单价
不超过6
 的部分
的部分2元/

超出6
 不超出10
不超出10 的部分
的部分4元/

超出10
 的部分
的部分8元

请根据上表的内容解答下列问题:
(1)填空:若该户居民2月份用水5
 ,则应交水费 元;3月份用水8
,则应交水费 元;3月份用水8 ,则应收水费 元;
,则应收水费 元;(2)若该户居民4月份用水
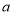
 (其中
(其中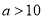 ),则应交水费多少元(用含
),则应交水费多少元(用含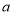 的代数式表示,并化简);
的代数式表示,并化简);(3)若该户居民5、6两个月共用水14
 (6月份用水量超过了5月份),设5月份用水
(6月份用水量超过了5月份),设5月份用水
 ,直接写出该户居民5、6两个月共交水费多少元(用含
,直接写出该户居民5、6两个月共交水费多少元(用含 的代数式表示).
的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 一组数据2,2,3,4,这组数据的中位数是2
B. 了解一批灯泡的使用寿命的情况,适合抽样调查
C. 小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分
D. 某日最高气温是
 ,最低气温是
,最低气温是 ,则该日气温的极差是
,则该日气温的极差是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,边AB、AC的垂直平分线分别交BC于E、F,若∠EAF=90°,AF=3,AE=4.
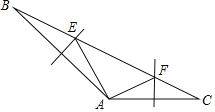
(1)求边BC的长;(2)求出∠BAC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠AOB=90°,OC平分∠AOB,点P在射线OC上.点E在射线OA上,点F在射线OB上,且∠EPF=90°.
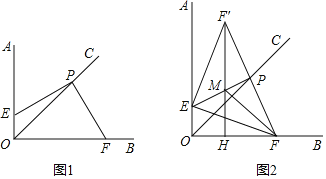
(1)如图1,求证:PE=PF;
(2)如图2,作点F关于直线EP的对称点F′,过F′点作FH⊥OF于H,连接EF′,F′H与EP交于点M.连接FM,图中与∠EFM相等的角共有 个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在数轴上点
 表示的数分别为-2,0,6,点
表示的数分别为-2,0,6,点 与点
与点 之间的距离表示为
之间的距离表示为 ,点
,点 与点
与点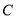 之间的距离表示为
之间的距离表示为 ,点
,点 与点
与点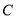 之间的距离表示为
之间的距离表示为 .
.(1)填空:
 ;
;(2)点
 开始在数轴上运动,若点
开始在数轴上运动,若点 以每秒1个单位长度的速度向左运动,同时,点
以每秒1个单位长度的速度向左运动,同时,点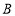 和点
和点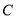 分别以每秒2个单位长度,5个单位长度的速度向右运动.
分别以每秒2个单位长度,5个单位长度的速度向右运动.①设运动时间为
 ,请用含有
,请用含有 的算式分别表示出
的算式分别表示出 ;
;②在①的条件下,
 的值是否随着时间
的值是否随着时间 的变化而变化?若变化,请说明理由;若不变,请求其值.
的变化而变化?若变化,请说明理由;若不变,请求其值.
相关试题

