【题目】如图,在平面直角坐标系中,点A(0,2),B(﹣2,0),点D是x轴上一个动点,以AD为一直角边在一侧作等腰直角三角形ADE,∠DAE=90°,若△ABD为等腰三角形时点E的坐标为 . 
参考答案:
【答案】(2,2)或(2,4)或(2,2 ![]() )或(2,﹣2
)或(2,﹣2 ![]() )
)
【解析】解:连接EC. 
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△BAD和△ACE中, ,
,
∴△ABD≌△ACE,
∴BD=EC.∠ABD=∠ACE=45°,
∵∠ACB=45°,
∴∠ECD=90°,
∴点E在过点C垂直x轴的直线上,且EC=DB,①当DB=DA时,点D与O重合,BD=OB=2,此时E(2,2).②当AB=AD时,BD=CE=4,此时E(2,4).③当BD=AB=2 ![]() 时,E(2,2
时,E(2,2 ![]() )或(2,﹣2
)或(2,﹣2 ![]() ),
),
故答案为(2,2)或(2,4)或(2,2 ![]() )或(2,﹣2
)或(2,﹣2 ![]() ).
).
连接EC.只要证明△ABD≌△ACE,推出BD=EC.∠ABD=∠ACE=45°,由∠ACB=45°,推出∠ECD=90°,推出点E在过点C垂直x轴的直线上,且EC=DB,再分三种情形讨论即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在暑假社会实践活动中,以每千克
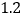 元的价格从批发市场购进若干千克西瓜市场上去销售,在销售了
元的价格从批发市场购进若干千克西瓜市场上去销售,在销售了 千克之后,余下的打折全部售完.销售金额
千克之后,余下的打折全部售完.销售金额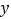 (元)售出西瓜的千克数
(元)售出西瓜的千克数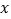 (千克)之间的关系如图所示.请你根据图像提供的信息完成以下问题:
(千克)之间的关系如图所示.请你根据图像提供的信息完成以下问题:(
 )求降价前销售金额
)求降价前销售金额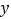 (元)与售出西瓜
(元)与售出西瓜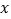 (千克)之间的关系;
(千克)之间的关系;(
 )小明这次社会实践活动赚了多少钱?
)小明这次社会实践活动赚了多少钱?(
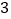 )若要使这次活动赚
)若要使这次活动赚 元钱,问余下的西瓜应打几折销售完?
元钱,问余下的西瓜应打几折销售完?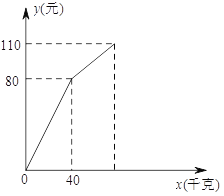
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式
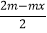 >
> x﹣1.
x﹣1.(1)当m=1时,求该不等式的解集;
(2)m取何值时,该不等式有解,并求出解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列图形,第一个图2条直线相交最多有1个交点,第二个图3条直线相交最多有3个交点,第三个图4条直线相交最多有6个交点,…,像这样,则20条直线相交最多交点的个数是( )

A. 171 B. 190 C. 210 D. 380
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
成绩频数分布表组别
成绩(分)
频数
A
50≤x<60
6
B
60≤x<70
m
C
70≤x<80
20
D
80≤x<90
36
E
90≤x<100
n

(1)频数分布表中的m= , n=;
(2)样本中位数所在成绩的级别是 , 扇形统计图中,E组所对应的扇形圆心角的度数是;
(3)若该校共有2000名学生,请你估计体育综合测试成绩不少于80分的大约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,AB的垂直平分线交AC于点N,交BC的延长线于点M,∠A=40°.
(1)求∠NMB的大小.
(2)如果将(1)中的∠A的度数改为70°,其余条件不变,再求∠NMB的大小.
(3)你认为存在什么样的规律?试用一句话说明.(请同学们自己画图)
(4)将(1)中的∠A改为钝角,对这个问题规律的认识是否需要加以修改?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.

(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD的形状,并说明理由.
相关试题

