【题目】提出问题:如图1,将三角板放在正方形ABCD上,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交边DC与点E,求证:PB=PE
分析问题:学生甲:如图1,过点P作PM⊥BC,PN⊥CD,垂足分别为M,N通过证明两三角形全等,进而证明两条线段相等.
学生乙:连接DP,如图2,很容易证明PD=PB,然后再通过“等角对等边”证明PE=PD,就可以证明PB=PE了.
解决问题:请你选择上述一种方法给予证明.
问题延伸:如图3,移动三角板,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交DC的延长线于点E,PB=PE还成立吗?若成立,请证明;若不成立,请说明理由.

参考答案:
【答案】解决问题:证明见解析;问题延伸:成立,证明见解析.
【解析】试题分析:对于图1,根据正方形的性质得∠BCD=90°,AC平分∠BCD,而PM⊥BC,PN⊥CD,则四边PMCN为矩形,根据角平分线性质得PM=PN,根据四边形内角和得到∠PBC+∠CEP=180°,再利用等角的补角相等得到∠PBM=∠PEN,然后根据“AAS”证明△PBM≌△PEN,则PB=PE;
对于图2,连结PD,根据正方形的性质得CB=CD,CA平分∠BCD,根据角平分线的性质得∠BCP=∠DCP,再根据“SAS”证明△CBP≌△CDP,则PB=PD,∠CBP=∠CDP,根据四边形内角和得到∠PBC+∠CEP=180°,再利用等角的补角相等得到∠PBC=∠PED,则∠PED=∠PDE,所以PD=PE,于是得到PB=PD;
对于图3,过点P作PM⊥BC,PN⊥CD,垂足分别为M,N,根据正方形的性质得∠BCD=90°,AC平分∠BCD,而PM⊥BC,PN⊥CD,得到四边PMCN为矩形,PM=PN,则∠MPN=90°,利用等角的余角相等得到∠BPM=∠EPN,然后根据“AAS”证明△PBM≌△PEN,所以PB=PE.
试题解析:证明:如图1,
∵四边形ABCD为正方形,
∴∠BCD=90°,AC平分∠BCD,
∵PM⊥BC,PN⊥CD,
∴四边PMCN为矩形,PM=PN,
∵∠BPE=90°,∠BCD=90°,
∴∠PBC+∠CEP=180°,
而∠CEP+∠PEN=180°,
∴∠PBM=∠PEN,
在△PBM和△PEN中

∴△PBM≌△PEN(AAS),
∴PB=PE;
如图2,连结PD,

∵四边形ABCD为正方形,
∴CB=CD,CA平分∠BCD,
∴∠BCP=∠DCP,
在△CBP和△CDP中
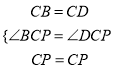 ,
,
∴△CBP≌△CDP(SAS),
∴PB=PD,∠CBP=∠CDP,
∵∠BPE=90°,∠BCD=90°,
∴∠PBC+∠CEP=180°,
而∠CEP+∠PEN=180°,
∴∠PBC=∠PED,
∴∠PED=∠PDE,
∴PD=PE,
∴PB=PD;
如图3,PB=PE还成立.

理由如下:过点P作PM⊥BC,PN⊥CD,垂足分别为M,N,
∵四边形ABCD为正方形,
∴∠BCD=90°,AC平分∠BCD,
∵PM⊥BC,PN⊥CD,
∴四边PMCN为矩形,PM=PN,
∴∠MPN=90°,
∵∠BPE=90°,∠BCD=90°,
∴∠BPM+∠MPE=90°,
而∠MEP+∠EPN=90°,
∴∠BPM=∠EPN,
在△PBM和△PEN中
 ,
,
∴△PBM≌△PEN(AAS),
∴PB=PE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD的两个顶点A、C在反比例函数
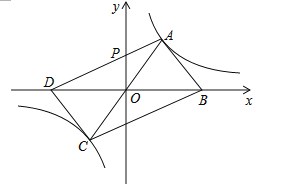
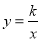 (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点(1)已知点A的坐标是(2,3),求k的值及C点的坐标;
(2)若△APO的面积为2,求点D到直线AC的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张老师买了一辆启辰R50X汽车,为了掌握车的油耗情况,在连续两次加油时做了如下工作:
①把油箱加满油;
②记录了两次加油时的累计里程(注:“累计里程”指汽车从出厂开始累计行驶的路程),以下是张老师连续两次加油时的记录:加油时间
加油量(升)
加油时的累计里程(千米)
2016年4月28日
18
6200
2016年5月16日
30
6600
则在这段时间内,该车每100千米平均耗油量为( )
A.3升
B.5升
C.7.5升
D.9升 -
科目: 来源: 题型:
查看答案和解析>>【题目】把61.235精确到0.01是;3.15万精确到位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分9分)学习了有理数的乘法后,老师给同学们布置这样一道题目:
计算49
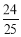 ×(–5),看谁算的又快又对,有两位同学的解法如下:
×(–5),看谁算的又快又对,有两位同学的解法如下:小明:原式=–
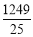 ×5=–
×5=–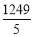 =–249
=–249 ;
;小军:原式=(49+
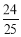 )×(–5)=49×(–5)+
)×(–5)=49×(–5)+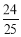 ×(–5)=–245–4
×(–5)=–245–4 =–249
=–249 ;
;(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19
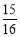 ×(–8).
×(–8). -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程a(x+m)2+n=0(a,m,n均为常数,m≠0)的解是x1=-2,x2=3,则方程a(x+m-5)2+n=0的解是( )
A. x1=-2,x2=3
B. x1=-7,x2=-2
C. x1=3,x2=-2
D. x1=3,x2=8
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程﹣x2+4mx+4=0的根的情况是( )
A. 没有实数根
B. 有两个相等的实数根
C. 有两个不相等的实数根
D. 不能确定
相关试题

