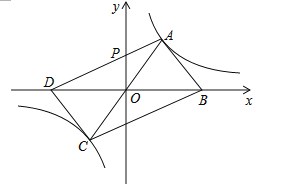
【题目】平行四边形ABCD的两个顶点A、C在反比例函数![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(1)已知点A的坐标是(2,3),求k的值及C点的坐标;
(2)若△APO的面积为2,求点D到直线AC的距离.
参考答案:
【答案】(1)k=6,C(﹣2,﹣3);(2)![]() .
.
【解析】
试题分析:(1)根据点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;
(2)根据△APO的面积为2,可以求得OP的长,从而可以求得点P的坐标,进而可以求得直线AP的解析式,从而可以求得点D的坐标,再根据等积法可以求得点D到直线AC的距离.
试题解析:(1)∵点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,∴3=
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,∴3=![]() ,点C与点A关于原点O对称,∴k=6,C(﹣2,﹣3),即k的值是6,C点的坐标是(﹣2,﹣3);
,点C与点A关于原点O对称,∴k=6,C(﹣2,﹣3),即k的值是6,C点的坐标是(﹣2,﹣3);
(2)∵△APO的面积为2,点A的坐标是(2,3),∴2=![]() ,得OP=2,设过点P(0,2),点A(2,3)的直线解析式为y=ax+b,则
,得OP=2,设过点P(0,2),点A(2,3)的直线解析式为y=ax+b,则![]() ,解得:
,解得:![]() ,即直线PC的解析式为
,即直线PC的解析式为![]() ,将y=0代入
,将y=0代入![]() ,得x═﹣4,∴OP=4,∵A(2,3),C(﹣2,﹣3),∴AC=
,得x═﹣4,∴OP=4,∵A(2,3),C(﹣2,﹣3),∴AC=![]() =
=![]() ,设点D到AC的距离为m,∵S△ACD=S△ODA+S△ODC,∴
,设点D到AC的距离为m,∵S△ACD=S△ODA+S△ODC,∴![]() ,解得,m=
,解得,m=![]() ,即点D到直线AC的距离是
,即点D到直线AC的距离是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式﹣3x2+mx+nx2﹣x+3的值与x无关,求(2m﹣n)2017的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年十一黄金周期间,九寨沟7天中每天旅游人数的变化情况如下表(正数表示比9月30日多的人数,负数表示比9月30日少的人数):
日期
1日
2日
3日
4日
5日
6日
7日
人数变化/万人
+0.5
+0.7
+0.8
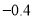
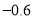
+0.2
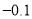
(1)、请判断7天内游客人数量最多和最少的各是哪一天?它们相差多少万人?(5分)
(2)、如果9月30日旅游人数为2.5万人,平均每人消费500元,请问风景区在此7天内总收入为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列特征量不能反映一组数据集中趋势的是( )
A.众数
B.中位数
C.方差
D.平均数 -
科目: 来源: 题型:
查看答案和解析>>【题目】张老师买了一辆启辰R50X汽车,为了掌握车的油耗情况,在连续两次加油时做了如下工作:
①把油箱加满油;
②记录了两次加油时的累计里程(注:“累计里程”指汽车从出厂开始累计行驶的路程),以下是张老师连续两次加油时的记录:加油时间
加油量(升)
加油时的累计里程(千米)
2016年4月28日
18
6200
2016年5月16日
30
6600
则在这段时间内,该车每100千米平均耗油量为( )
A.3升
B.5升
C.7.5升
D.9升 -
科目: 来源: 题型:
查看答案和解析>>【题目】把61.235精确到0.01是;3.15万精确到位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】提出问题:如图1,将三角板放在正方形ABCD上,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交边DC与点E,求证:PB=PE
分析问题:学生甲:如图1,过点P作PM⊥BC,PN⊥CD,垂足分别为M,N通过证明两三角形全等,进而证明两条线段相等.
学生乙:连接DP,如图2,很容易证明PD=PB,然后再通过“等角对等边”证明PE=PD,就可以证明PB=PE了.
解决问题:请你选择上述一种方法给予证明.
问题延伸:如图3,移动三角板,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交DC的延长线于点E,PB=PE还成立吗?若成立,请证明;若不成立,请说明理由.

相关试题

