搜索
【题目】从2018年高中一年级学生开始，湖南省全面启动高考综合改革，学生学习完必修课程后，可以根据高校相关专业的选课要求和自身兴趣、志向、优势，从思想政治、历史、地理、物理、化学、生物6个科目中，自主选择3个科目参加等级考试.学生
已选物理，还想从思想政治、历史、地理3个文科科目中选1科，再从化学、生物2个理科科目中选1科.若他选思想政治、历史、地理的可能性相等，选化学、生物的可能性相等，则选修地理和生物的概率为___________.
参考答案：
【答案】
【解析】列表格得出所有等可能的情况，然后再找出符合题意的情况，根据概率公式进行计算即可得.
政治 | 历史 | 地理 | |
化学 | 化学，政治 | 化学，历史 | 化学，地理 |
生物 | 生物，政治 | 生物，历史 | 生物，地理 |
从表格中可以看出一共有6种等可能的情况，选择地理和生物的有1种情况，
所以选择地理和生物的概率是，
故答案为：.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，∠B=90°AB∥DF，AB=3cm，BD=8cm，点C是线段BD上一动点，点E是直线DF上一动点，且始终保持AC⊥CE。
（1）试说明：∠ACB =∠CED
（2）当C为BD的中点时，
ABC与
EDC全等吗？若全等，请说明理由；若不全等，请改变BD的长（直接写出答案），使它们全等。（3）若AC=CE ,试求DE的长
（4）在线段BD的延长线上，是否存在点C，使得AC=CE，若存在，请求出DE的长及△AEC的面积；若不存在，请说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】为弘扬中华传统文化，黔南州近期举办了中小学生“国学经典大赛”，比赛项目为：A．唐诗；B．宋词；C．论语；D．三字经．比赛形式为两人对抗赛，即把四种比赛项目写在4张完全相同的卡片上，比赛时，比赛的两人从中随机抽取1张卡片作为自己的比赛项目（不放回，且每人只能抽取一次）比赛时，小红和小明分到一组．（1）小明先抽取，那么小明抽到唐诗的概率是多少？
（2）小红擅长唐诗，小红想：“小明先抽取，我后抽取”抽到唐诗的概率是不同的，且小明抽到唐诗的概率更大，若小红后抽取，小红抽中唐诗的概率是多少？小红的想法对吗？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（ ）
A.带①去B.带②去C.带③去D.带①和②去
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面的文字后，解答问题：
有这样一道题目：“如图，E、D是△ABC中BC边上的两点，AD＝AE， ．求证△ABE≌△ACD．请根据你的理解，在题目中的空格内，把原题补充完整（添加一个适当的条件），并写出证明过程．
-
科目： 来源： 题型：
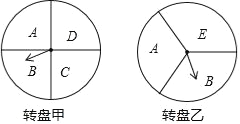
查看答案和解析>>【题目】某超市在端午节期间开展优惠活动，凡购物者可以通过转动转盘的方式享受折扣优惠，本次活动共有两种方式，方式一：转动转盘甲，指针指向 A区域时，所购买物品享受9折优惠、指针指向其它区域无优惠；方式二： 同时转动转盘甲和转盘乙，若两个转盘的指针指向每个区域的字母相同，所购买物品享受8折优惠，其它情况无优惠．在每个转盘中，指针指向每个区城的可能性相同（若指针指向分界线，则重新转动转盘）
(1)若顾客选择方式一，则享受 9 折优惠的概率为_______；
(2)若顾客选择方式二，请用树状图或列表法列出所有可能，并求顾客享受8折优惠的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，ACB和DCE都是等腰直角三角形，∠ACB=∠DCE=90
，连接AE、BD交于点O. AE与DC交于点M，BD与AC交于点N.（1）如图①，求证：AE=BD；
（2）如图②，若AC=DC，在不添加任何辅助线的情况下，请直接写出图②中四对全等的直角三角形.
相关试题
