【题目】如图,已知⊙O的直径AB与弦CD相交于点E,AB⊥CD,⊙O的切线BF与弦AD的延长线相交于点F.
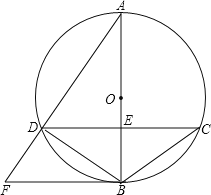
(1)求证:CD∥BF;
(2)若⊙O的半径为5,cos∠BCD=![]() ,求线段AD的长.
,求线段AD的长.
参考答案:
【答案】(1)证明见解析;(2)AD=8.
【解析】
试题分析:(1)由BF是⊙O的切线,AB是⊙O的直径,根据切线的性质,即可得BF⊥AB,又由AB⊥CD,即可得CD∥BF;
(2)又由AB是⊙O的直径,可得∠ADB=90°,由圆周角定理,可得∠BAD=∠BCD,然后由⊙O的半径为5,cos∠BCD=![]() ,即可求得线段AD的长.
,即可求得线段AD的长.
(1)证明:∵BF是⊙O的切线,AB是⊙O的直径,
∴BF⊥AB,
∵CD⊥AB,
∴CD∥BF;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵⊙O的半径5,
∴AB=10,
∵∠BAD=∠BCD,
∴cos∠BAD=cos∠BCD=![]() =
=![]() ,
,
∴AD=cos∠BADAB=![]() ×10=8,
×10=8,
∴AD=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣2的绝对值是( )
A.2 B.﹣2 C.±2 D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种水果第一天以2元的价格卖出
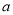 斤,第二天以1.5元的价格卖出
斤,第二天以1.5元的价格卖出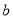 斤,第三天以1.2元的价格卖出
斤,第三天以1.2元的价格卖出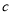 斤,求:
斤,求:(1)、这三天共卖出水果多少斤?
(2)、这三天共卖得多少元?
(3)、这三天平均售价是多少?并计算当
 =30,
=30,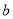 =40,
=40,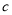 =50时,平均售价是多少?
=50时,平均售价是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4 cm,BC=8 cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5 cm,点Q的速度为每秒4 cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为
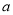 、
、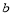 (单位:cm,
(单位:cm,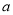
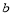 ≠0),已知A、C、P、Q四点为顶 点的四边形是平行四边形,求
≠0),已知A、C、P、Q四点为顶 点的四边形是平行四边形,求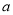 与
与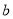 满足的数量关系式.
满足的数量关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
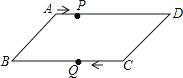
A.4次 B.3次 C.2次 D.1次
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点(a,b)在一次函数y=2x﹣3上,则代数式3b﹣6a+1的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,…, 则32018的末位数字是( )
A. 9 B. 1 C. 3 D. 7
相关试题

