【题目】某种水果第一天以2元的价格卖出![]() 斤,第二天以1.5元的价格卖出
斤,第二天以1.5元的价格卖出![]() 斤,第三天以1.2元的价格卖出
斤,第三天以1.2元的价格卖出![]() 斤,求:
斤,求:
(1)、这三天共卖出水果多少斤?
(2)、这三天共卖得多少元?
(3)、这三天平均售价是多少?并计算当![]() =30,
=30,![]() =40,
=40,![]() =50时,平均售价是多少?
=50时,平均售价是多少?
参考答案:
【答案】(1)、(a+b+c)斤;(2)、(2a+1.5b+1.2c)元;(3)、1.5元/斤.
【解析】
试题分析:(1)、将三天所卖出的水果数量进行相加得出总数;(2)、根据售价×数量得出每天的营业额,然后进行相加得出答案;(3)、平均售价=三天总的钱÷三天总的数量得出答案,然后将a、b、c的值代入代数式进行计算,得出答案.
试题解析:(1)、(a+b+c)斤
(2)、(2a+1.5b+1.2c)元
(3)、这三天平均售价是![]() 元/斤
元/斤
当![]() =30,
=30,![]() =40,
=40,![]() =50时,
=50时,
原式![]()
![]()
![]()
![]()
答:平均售价是![]() 元/斤.
元/斤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【知识背景】在学习计算框图时,可以用“
 ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条)
【尝试解决】
(1)①如图1,当输入数x=﹣2时,输出数y=__________;
②如图2,第一个“
 ”内,应填__________; 第二个“
”内,应填__________; 第二个“ ”内,应填__________;
”内,应填__________;(2)①如图3,当输入数x=﹣1时,输出数y=__________;②如图4,当输出的值y=17,则输入的值x=__________;
【实际应用】
(3)为鼓励节约用水,决定对用水实行“阶梯价”:当每月用水量不超过10吨时(含10吨),以3元/吨的价格收费;当每月用水量超过10吨时,超过部分以4元/吨的价格收费.请设计出一个“计算框图”,使得输入数为用水量x,输出数为水费y.
-
科目: 来源: 题型:
查看答案和解析>>【题目】去括号正确的是( )
A. -(a+b-c)=-a+b-c
B. -2(a+b-3c)=-2a-2b+6c
C. -(-a-b-c)=-a+b+c
D. -(a-b-c)=-a+b-c
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣2的绝对值是( )
A.2 B.﹣2 C.±2 D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4 cm,BC=8 cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5 cm,点Q的速度为每秒4 cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为
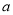 、
、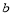 (单位:cm,
(单位:cm,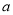
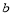 ≠0),已知A、C、P、Q四点为顶 点的四边形是平行四边形,求
≠0),已知A、C、P、Q四点为顶 点的四边形是平行四边形,求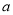 与
与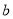 满足的数量关系式.
满足的数量关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AB与弦CD相交于点E,AB⊥CD,⊙O的切线BF与弦AD的延长线相交于点F.
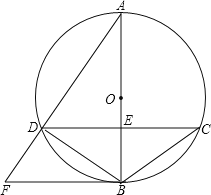
(1)求证:CD∥BF;
(2)若⊙O的半径为5,cos∠BCD=
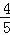 ,求线段AD的长.
,求线段AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
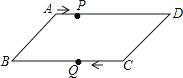
A.4次 B.3次 C.2次 D.1次
相关试题

