【题目】某校为了解全校2000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成频数分布直方图(如图所示). 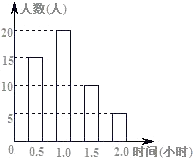
(1)这50名学生在这一天课外阅读所用时间的众数是多少?
(2)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(3)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
参考答案:
【答案】
(1)解:众数是1.0(小时)
(2)解:x= ![]() (0.5×15+1.0×20+1.5×10+2.0×5)=1.05(小时),
(0.5×15+1.0×20+1.5×10+2.0×5)=1.05(小时),
这50名学生在这一天平均每人的课外阅读所用时间是1.05小时
(3)解:2000× ![]() =1400,
=1400,
所以全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的约为1400人
【解析】(1)根据众数的概念:出现次数最多的数据,即1.0出现的次数最多,是20次.所以众数是1.0;(2)根据加权平均数进行正确计算;(3)首先计算样本中这一天课外阅读所用时间在1.0小时以上的频率,再进一步计算全校学生中在这一天课外阅读所用时间在1.0小时以上的人数.
【考点精析】利用频数分布直方图和算术平均数对题目进行判断即可得到答案,需要熟知特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图);总数量÷总份数=平均数.解题关键是根据已知条件确定总数量以及与它相对应的总份数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】x是数轴上任意一点表示的数,若|x﹣3|+|x+2|的值最小,则x的取值范围是( )
A. x≥3B. x≤﹣2C. ﹣2≤x≤3D. ﹣2<x<3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:正方形ABCD中,AB=8,点O为边AB上一动点,以点O为圆心,OB为半径的⊙O交边AD于点E(不与点A、D重合),EF⊥OE交边CD于点F.设BO=x,AE=y.
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)在点O运动的过程中,△EFD的周长是否发生变化?如果发生变化,请用x的代数式表示△EFD的周长;如果不变化,请求出△EFD的周长;
(3)以点A为圆心,OA为半径作圆,在点O运动的过程中,讨论⊙O与⊙A的位置关系,并写出相应的x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)( )﹣1+(
)﹣1+(  )2×(﹣2)3﹣(π﹣3)0 .
)2×(﹣2)3﹣(π﹣3)0 .
(2)4xy2(﹣ x2yz3).
x2yz3). -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程(a+2)x2-2ax+a2-4=0的一个根为0,则a=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
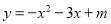 经过点C(-2,6),
经过点C(-2,6),与x轴相交于A、B两点(A在B的左侧),与y轴交于点D.
(1)求点A的坐标;
(2)设直线BC交y轴于点E,连接AE、AC,求证:
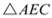 是等腰直角三角形;
是等腰直角三角形;(3)连接AD交BC于点F,试问当
 时,在抛物线上是否存在一点P使得以A、B、P为顶点的三角形与
时,在抛物线上是否存在一点P使得以A、B、P为顶点的三角形与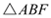 相似?若存在, 请求出点P的坐标;若不存在,请说明理由.
相似?若存在, 请求出点P的坐标;若不存在,请说明理由.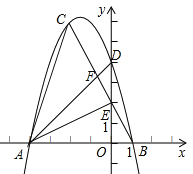
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若AC=2,
 , 求菱形ABCD的面积.
, 求菱形ABCD的面积.
相关试题

