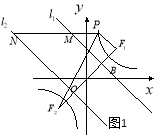
【题目】如图1所示，已知：点在双曲线：上，直线，直线与关于原点成中心对称，两点间的连线与曲线第一象限内的交点为，是曲线上第一象限内异于的一动点，过作轴平行线分别交，于两点.

（1）求双曲线及直线的解析式；

（2）求证：；

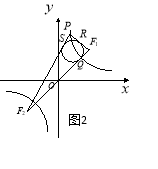
（3）如图2所示，的内切圆与三边分别相切于点，求证：点与点重合.（参考公式：在平面坐标系中，若有点，，则A、B两点间的距离公式为=.

参考答案：

【答案】（1），；（2）详见解析；（3）详见解析.

【解析】

试题分析：（1）把A点坐标代入可求得a值，即可得双曲线C的解析式，易得与轴的交点分别是，可求得与轴的交点关于原点对称点的坐标分别为，即可得直线的解析式；（2）设，根据两点间的距离公式证明出，，所以；（3）与三别分别相切于点所以PR=PS,,可得，又因，所以QO=2而即点与点重合.

试题解析：（1）解：

与轴的交点分别是，它们关于原点的对称点分别是

（2）设

，

同理

因此

（3）与三别分别相切于点

又，

而

所以，点与点重合.（第三问如果计算得出，并且点与点都在线段内，那么也可以证明点与点重合）

关闭