Question

【题目】抛物线y=ax2+bx+c（a≠0）与x轴交于A（2，0），B（4，0）两点，与y轴交于点C（0，2）．

（1）求抛物线的解析式；
（2）点P从点O出发，乙每秒2个单位长度的速度向点B运动，同时点E也从点O出发，以每秒1个单位长度的速度向点C运动，设点P的运动时间t秒（0＜t＜2）．
①过点E作x轴的平行线，与BC相交于点D（如图所示），当t为何值时， 的值最小，求出这个最小值并写出此时点E、P的坐标；
②在满足①的条件下，抛物线的对称轴上是否存在点F，使△EFP为直角三角形？若存在，请直接写出点F的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：∵y=ax2+bx+c（a≠0）与x轴交于A（2，0），B（4，0）两点，与y轴交于点C（0，2）．

∴ ，

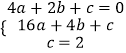解得：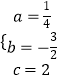

∴抛物线的解析式为y= x2﹣ x+2．

（2）

解：①由题意得：OP=2t，OE=t，

∵DE∥OB，

∴△CDE∽△CBO，

∴ ，即 ，

∴DE=4﹣2t，

∴ ，

∵0＜t＜2，1﹣（t﹣1）2始终为正数，且t=1时，1﹣（t﹣1）2有最大值1，

∴t=1时， 有最小值1，即t=1时， 有最小值1，此时OP=2，OE=1，

∴E（0，1），P（2，0）；

②存在，

∵抛物线y= x2﹣ x+2的对称轴方程为x=3，

设F（3，m），

∴EP2=5，PF2=（3﹣2）2+m2，EF2=（m﹣1）2+32，

当△EFP为直角三角形时，

（a）当∠EPF=90°时，

EP2+PF2=EF2，

即5+1+m2=（m﹣1）2+32，

解得：m=2，

（b）当∠EFP=90°时，

EF2+FP2=PE2，

即（m﹣1）2+32+（3﹣2）2+m2=5，

此方程无解，不合题意舍去，

∴当∠EFP=90°时，

这种情况不存在，

（c）当∠PEF=90°时，

EF2+PE2=PF2，

即（m﹣1）2+32+5=（3﹣2）2+m2，

解得：m=7，

∴F（3，2），（3，7）．

【解析】（1）利用待定系数法求函数解析式即可；（2）①由题意得：OP=2t，OE=t，通过△CDE∽△CBO得到 ，即 ，求得 有最小值1，即可求得结果；②存在，求得抛物线y= x2﹣ x+2的对称方程为x=3，设F（3，m），当△EFP为直角三角形时（a）当∠EPF=90°时，（b）当∠EFP=90°时，（c）当∠PEF=90°时，根据勾股定理列方程即可求得结果．
【考点精析】通过灵活运用二次函数的图象和二次函数的性质，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小即可以解答此题．