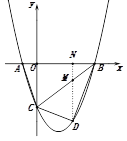
【题目】已知:如图,抛物线y=![]() x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
(1)求抛物线的解析式;
(2)若点D是线段BC下方抛物线上的动点,求四边形ABCD面积的最大值;
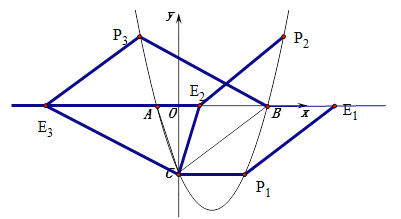
(3)若点E在x轴上,点P在抛物线上.是否存在以B、C、E、P为顶点且以BC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.


参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)P1(3,-3),P2(
;(3)P1(3,-3),P2(![]() ,3),P3(
,3),P3(![]() ,3).
,3).
【解析】试题分析:(1)将![]() 的坐标代入抛物线中,求出待定系数的值,即可得出抛物线的解析式.
的坐标代入抛物线中,求出待定系数的值,即可得出抛物线的解析式.
(2)根据![]() 的坐标,易求得直线
的坐标,易求得直线![]() 的解析式.由于
的解析式.由于![]() 都是定值,则
都是定值,则![]() 的面积不变,若四边形
的面积不变,若四边形![]() 面积最大,则
面积最大,则![]() 的面积最大;过点
的面积最大;过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,则
,则![]() 可得到当
可得到当![]() 面积有最大值时,四边形
面积有最大值时,四边形![]() 的面积最大值.
的面积最大值.
(3)本题应分情况讨论:①过![]() 作
作![]() 轴的平行线,与抛物线的交点符合
轴的平行线,与抛物线的交点符合![]() 点的要求,此时
点的要求,此时![]() 的纵坐标相同,代入抛物线的解析式中即可求出
的纵坐标相同,代入抛物线的解析式中即可求出![]() 点坐标;②将
点坐标;②将![]() 平移,令
平移,令![]() 点落在
点落在![]() 轴(即
轴(即![]() 点)、
点)、![]() 点落在抛物线(即
点落在抛物线(即![]() 点)上;可根据平行四边形的性质,得出
点)上;可根据平行四边形的性质,得出![]() 点纵坐标(
点纵坐标(![]() 纵坐标的绝对值相等),代入抛物线的解析式中即可求得
纵坐标的绝对值相等),代入抛物线的解析式中即可求得![]() 点坐标.
点坐标.
试题解析:(1)把![]() 代入
代入![]() ,
,
可以求得![]()
∴![]()
(2)过点![]() 作
作![]() 轴分别交线段
轴分别交线段![]() 和
和![]() 轴于点
轴于点![]() ,
,
在![]() 中,令
中,令![]() ,得
,得![]()
![]()
设直线![]() 的解析式为
的解析式为![]()
可求得直线![]() 的解析式为:
的解析式为: ![]()
∵S四边形ABCD![]()
设![]()
![]()
![]()
当![]() 时,
时, ![]() 有最大值
有最大值![]()
此时四边形ABCD面积有最大值![]()
(3)如图所示,
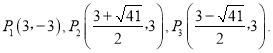
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时)
挖掘土石方量(单位:m3/台时)
甲型挖掘机
100
60
乙型挖掘机
120
80
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有
 个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为
个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为 人次,公园游戏场发放的福娃玩具为
人次,公园游戏场发放的福娃玩具为 个.
个. 求参加一次这种游戏活动得到福娃玩具的概率;
求参加一次这种游戏活动得到福娃玩具的概率; 请你估计袋中白球接近多少个?
请你估计袋中白球接近多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.
(1)求证:△PFA∽△ABE;
(2)当点P在线段AD上运动时,设PA=x,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由;
(3)探究:当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,请直接写出x满足的条件: .

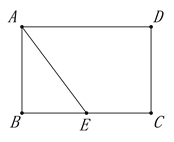
备用图
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示,下面有四个推断:
①二次函数y1有最大值;
②二次函数y1的图象关于直线x=﹣1对称
③当x=﹣2时,二次函数y1的值大于0
④过动点P(m,0)且垂直于x轴的直线与y1,y2的图象的交点分别为C,D,当点C位于点D上方时,m的取值范围是m<﹣3或m>﹣1.
以上推断正确的是( )
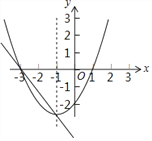
A. ①③ B. ①④ C. ②③ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO
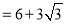 ;⑤S△AOC+S△AOB=
;⑤S△AOC+S△AOB=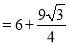 .其中正确的结论是( )
.其中正确的结论是( )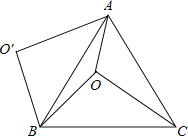
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
-
科目: 来源: 题型:
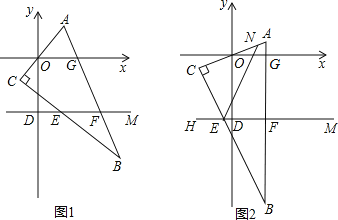
查看答案和解析>>【题目】在平面直角坐标系中,D(0,-3),M(4,-3),直角三角形ABC的边与x轴分别交于O、G两点,与直线DM分别交于E、F点.
(1)将直角三角形ABC如图1位置摆放,请写出∠CEF与∠AOG之间的等量关系:______.
(2)将直角三角形ABC如图2位置摆放,N为AC上一点,∠NED+∠CEF=180°,请写出∠NEF与∠AOG之间的等量关系,并说明理由.
相关试题

