【题目】如图1,在ABCD中,AF平分∠BAD交BC于点F,CE平分∠BCD交AD于点E.

图1 图2
(1)求证:四边形AFCE是平行四边形;
(2)如图2,若BE⊥EC,求证:四边形ABFE是菱形.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)直接利用角平分线的性质再结合平行四边形的性质进而得出AF∥EC,即可得出答案;
(2)直接利用全等三角形的判定与性质得出AO=FO,BO=EO,进而得出答案.
证明:(1)∵AF平分∠BAD,CE平分∠BCD,
∴∠FAE=![]() ∠BAE,∠FCE=
∠BAE,∠FCE=![]() ∠FCD.
∠FCD.
∵四边形ABCD是平行四边形,
∴∠BAE=∠FCD,AD∥BC.
∴∠FAE=∠FCE,∠FCE=∠CED.
∴∠FAE=∠CED.
∴AF∥EC.
又∵AE∥CF,
∴四边形AFCE为平行四边形.
(2)∵AF∥EC,BE⊥EC,
∴∠AOE=∠BEC=90°.
∴∠AOE=∠AOB=90°.
在△ABO和△AEO中,
 ,
,
∴△ABO≌△AEO(ASA).
∴BO=EO.
同理可得△ABO≌△FBO,
∴AO=FO.
∴四边形ABFE是平行四边形.
又∵AF⊥BE,
∴平行四边形ABFE是菱形.
-
科目: 来源: 题型:
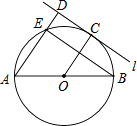
查看答案和解析>>【题目】如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC、BE.若AE=6,OA=5,则线段DC的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有学生55人,其中男生与女生的人数之比为6:5。
(1)求出该班男生与女生的人数;
(2)学校要从该班选出20人参加学校的合唱团,要求:①男生人数不少于7人;②女生人数超过男生人
数2人以上。请问男、女生人数有几种选择方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
-
科目: 来源: 题型:
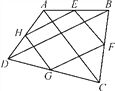
查看答案和解析>>【题目】如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点.
(1)当四边形ABCD是矩形时,四边形EFGH是_________,请说明理由;
(2)当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件下,不能判定△ABC≌△A′B′C′是( )
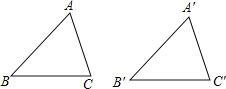
A. ∠A=∠A′,AB=A′B′,BC=B′C′ B. ∠A=∠A′,∠C=∠C′,AC=A′C′
C. ∠B=∠B′,∠C=∠C′,AC=A′C′ D. BA=B′A′,BC=B′C′,AC=A′C′
相关试题

