【题目】(本题满分10分)如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,M为边AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.试说明BD与MF的位置关系,并说明理由.

参考答案:
【答案】BD∥MF
【解析】试题分析:根据角平分线的定义与四边形的内角和定理求出∠ABD+∠AMF=90°,又∠AFM+∠AMF=90°,得到∠ABD=∠AFM,然后根据同位角相等,两直线平行可得BD∥MF.
试题解析:解: BD∥MF.理由如下:
∵∠A=90°,ME⊥BC,∴∠ABC+∠AME=360°﹣90°×2=180°.∵BD平分∠ABC,MF平分∠AME,∴∠ABD=![]() ∠ABC,∠AMF=
∠ABC,∠AMF=![]() ∠AME,∴∠ABD+∠AMF=
∠AME,∴∠ABD+∠AMF=![]() (∠ABC+∠AME)=90°.又∵∠AFM+∠AMF=90°,∴∠ABD=∠AFM,∴BD∥MF.
(∠ABC+∠AME)=90°.又∵∠AFM+∠AMF=90°,∴∠ABD=∠AFM,∴BD∥MF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)根据下列叙述填依据:
已知:如图①,AB∥CD,∠B+∠BFE=180°,求∠B+∠BFD+∠D的度数.
解:因为∠B+∠BFE=180°,
所以AB∥EF( ).
又因为AB∥CD,
所以CD∥EF( ).
所以∠CDF+∠DFE=180°( ).
所以∠B+∠BFD+∠D=∠B+∠BFE+∠DFE+∠D=360°.
(2)根据以上解答进行探索:如图②,AB∥EF,∠BDF与∠B,∠F有何数量关系?并说明理由.
(3)如图③④,AB∥EF,你能探索出图③、图④两个图形中,∠BDF与∠B,∠F的数量关系吗?请直接写出结果.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“手机使用目的”和“每周使用手机时间”的问卷调查,并绘制成如图①②的统计图。已知“查资料”人人数是40人。

请你根据以上信息解答以下问题
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是_______________。
(2)补全条形统计图
(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 (1),已知△ABC是等边三角形,以BC为直径的⊙O交AB、AC于D、E.求证:

(1)△DOE是等边三角形.
(2)如图(2),若∠A=60°,AB≠AC, 则(1)中结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
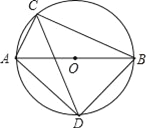
-
科目: 来源: 题型:
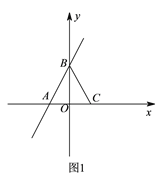
查看答案和解析>>【题目】如图
 ,在平面直角坐标系
,在平面直角坐标系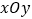 中,一次函数
中,一次函数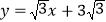 的图象与
的图象与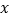 轴交于点
轴交于点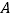 ,与
,与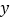 轴交于点
轴交于点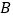 ,点
,点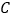 的坐标为
的坐标为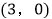 ,连接
,连接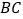 .
.
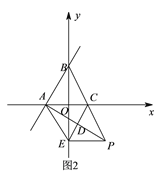
(
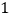 )求证:
)求证: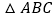 是等边三角形.
是等边三角形.(
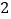 )点
)点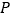 在线段
在线段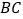 的延长线上,连接
的延长线上,连接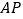 ,作
,作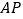 的垂直平分线,垂足为点
的垂直平分线,垂足为点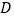 ,并与
,并与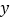 轴交于点
轴交于点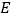 ,分别连接
,分别连接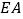 、
、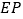 .
.①如图
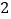 ,若
,若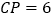 ,直接写出
,直接写出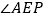 的度数.
的度数.②若点
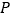 在线段
在线段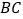 的延长线上运动(
的延长线上运动(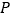 与点
与点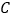 不重合),
不重合),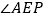 的度数是否变化?若变化,请说明理由;若不变,求出
的度数是否变化?若变化,请说明理由;若不变,求出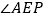 的度数.
的度数.(
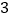 )在(
)在(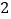 )的条件下,若点
)的条件下,若点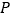 从点
从点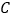 出发在
出发在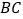 的延长线上匀速运动,速度为每秒
的延长线上匀速运动,速度为每秒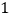 个单位长度,
个单位长度,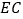 与
与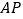 交于点
交于点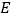 ,设
,设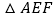 的面积为
的面积为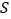 ,
,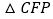 的面积为
的面积为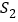 ,
,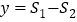 ,运动时间为
,运动时间为 秒时.求
秒时.求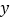 关于
关于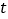 的函数关系式.
的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下两幅统计图.请根据相关信息,解答下列问题:

(1)扇形统计图中a= ,初赛成绩为1.70m所在扇形图形的圆心角为
(2)补全条形统计图;
(3)这组初赛成绩的众数是 m,中位数是 ;
(4)根据这组初赛成绩确定8人进入复赛,那么初赛成绩为1.60m的运动员杨强能否进入复赛?为什么?
相关试题

