【题目】如图,抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.

参考答案:
【答案】(1)![]() ;(2)D的坐标是(1,﹣4),对称轴是直线x=1;(3)P(1,
;(2)D的坐标是(1,﹣4),对称轴是直线x=1;(3)P(1,![]() )或(1,
)或(1,![]() )或(1,
)或(1,![]() )或(1,4).
)或(1,4).
【解析】
试题分析:(1)根据抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),可以求得抛物线的解析式;
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),可以求得抛物线的解析式;
(2)根据(1)中的解析式化为顶点式,即可得到此抛物线顶点D的坐标和对称轴;
(3)首先写出存在,然后运用分类讨论的数学思想分别求出各种情况下点P的坐标即可.
试题解析:(1)∵抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),∴
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),∴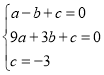 ,解得:
,解得: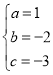 ,即此抛物线的解析式是
,即此抛物线的解析式是![]() ;
;
(2)∵![]() =
=![]() ,∴此抛物线顶点D的坐标是(1,﹣4),对称轴是直线x=1;
,∴此抛物线顶点D的坐标是(1,﹣4),对称轴是直线x=1;
(3)存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形,设点P的坐标为(1,y),分三种情况讨论:
①当PA=PD时![]() =
=![]() ,解得,y=
,解得,y=![]() ,即点P的坐标为(1,
,即点P的坐标为(1,![]() );
);
②当DA=DP时,![]() =
=![]() ,解得,y=
,解得,y=![]() ,即点P的坐标为(1,
,即点P的坐标为(1,![]() )或(1,
)或(1,![]() );
);
③当AD=AP时,![]() =
=![]() ,解得,y=±4,即点P的坐标是(1,4)或(1,﹣4),当点P为(1,﹣4)时与点D重合,故不符合题意.
,解得,y=±4,即点P的坐标是(1,4)或(1,﹣4),当点P为(1,﹣4)时与点D重合,故不符合题意.
由上可得,以点P、D、A为顶点的三角形是等腰三角形时,点P的坐标为(1,![]() )或(1,
)或(1,![]() )或(1,
)或(1,![]() )或(1,4).
)或(1,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2﹣ab=20,ab﹣b2=﹣12,则a2﹣b2= , a2﹣2ab+b2= .
-
科目: 来源: 题型:
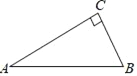
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°.
(1)用圆规和直尺在AC上作点P,使点P到A、B的距离相等.(保留作图痕迹,不写作法和证明)
(2)当满足(1)的点P到AB、BC的距离相等时,求∠A的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程

(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长为
 ,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种水果的进价为4.5元/千克,销售中估计有10%的正常损耗,商家为了避免亏本,售价至少应定为_____元/千克.
-
科目: 来源: 题型:
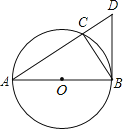
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D。
(1)求证:△ABC∽△BDC。
(2)若AC=8,BC=6,求△BDC的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一直角三角形的木版,三边的平方和为1800cm2,则斜边长为( )
A. 80cm B. 30cm C. 90cm D. 120cm
相关试题

