【题目】解方程组:(1)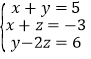 ;
;
(2)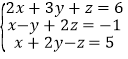 ;
;
(3)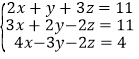 ;
;
(4)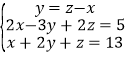 .
.
参考答案:
【答案】(1) ;(2)
;(2)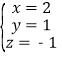 ;(3)
;(3)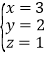 ;(4)
;(4)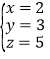 .
.
【解析】
(1)由①-②消去x,与③组成y、z的二元一次方程组,进一步解二元一次方程组,求得答案即可;
(2)③+①消去z,③×2+②消去z,组成关于x、y的二元一次方程组,进一步解二元一次方程组,求得答案即可;
(3)①×2-②消去y,①×3+③消去y,组成关于x、z的二元一次方程组,进一步解二元一次方程组,求得答案即可;
(4)把①代入②消去y,把①代入③,消去y,组成关于x、z的二元一次方程组,进一步解二元一次方程组,求得答案即可.
(1)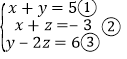
由①-②,得y-z=8.④
④-③,得z=2.
把z=2代入④,得y=10.把y=10代入①,得x=-5.
所以,原方程组的解为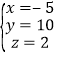 ;
;
(2)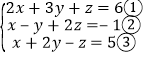
③+①,得3x+5y=11.④
③×2+②,得3x+3y=9.⑤
④-⑤,得2y=2,y=1.
将y=1代入⑤,得3x=6,x=2.
将x=2,y=1代入①,得z=6-2×2-3×1=-1,
所以原方程组的解为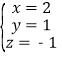 ;
;
(3)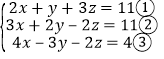 ,
,
①×2-②,得x+8z=11.④
①×3+③,得10x+7z=37.⑤
解由④与⑤组成的方程组,得![]() ,
,
把x=3,z=1代入①,得y=2.
所以原方程组的解为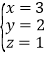 ;
;
(4)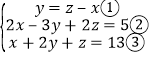 ,
,
把①代入②,得2x-3z+3x+2z=5,
即5x-z=5④
把①代入③,得x+2z-2x+z=13,
即3z-x=13.⑤
④×3+⑤,得14x=28,所以x=2.
把x=2代入④,得z=5.
把x=2,z=5代入①,得y=3.
所以原方程组的解是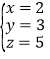
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=(2m+1)x+m﹣3
(1)若函数图象经过原点,求m的值;
(2)若函数图象与y轴的交点坐标为(0,﹣2),求m的值;
(3)若y随着x的增大而增大,求m的取值范图;
(4)若函数图象经过第一、三,四象限,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有( )
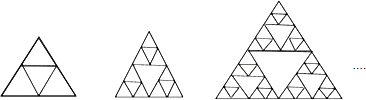
A.160
B.161
C.162
D.163 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 .
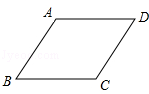
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算:|﹣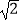 |+(
|+(  )﹣1﹣2cos45°.
)﹣1﹣2cos45°.
(2)解方程: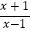 +
+ 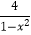 =1.
=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电器公司计划装运甲、乙、丙三种家电到农村销售(规定每辆汽车按规定满载,且每辆汽车只能装同一种家电).下表所示为装运甲、乙、丙三种家电的台数及利润.
甲
乙
丙
每辆汽车能装运的台数
40
20
30
每台家电可获利润(万元)
0.05
0.07
0.04
(1)若用8辆汽车装运乙、丙两种家电190台到A地销售,问装运乙、丙的汽车各多少辆.
(2)计划用20辆汽车装运甲、乙、丙三种家电720台到B地销售,如何安排装运,可使公司获得36.6万元的利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程y(米)与小张出发后的时间x(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时y与x之间的函数表达式;
(3)求小张与小李相遇时x的值.

相关试题

