【题目】某自行车厂一周计划生产![]() 辆自行车,平均每天生产自行车
辆自行车,平均每天生产自行车![]() 辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入.下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负.单位:辆):
辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入.下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负.单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产自行车__________辆.
(2)产量最多的一天比产量最少的一天多生产__________辆.
(3)该厂实行按生产的自行车数量的多少计工资,即计件工资制.每生产一辆自行车可以得人民币![]() 元,若超额完成任务,则超出部分,每辆
元,若超额完成任务,则超出部分,每辆![]() 元;若不足计划数的,每少生产一辆扣
元;若不足计划数的,每少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?
参考答案:
【答案】(1)362;(2)30;(3)50850元.
【解析】
(1)分别表示出前三天的自行车生产数量,再求其和即可;
(2)根据生产情况:用产量最高的一天减产量最低的一天即可;
(3)先计算超额完成几辆,然后再计算工资即可.
解:(1)120+6+(1203)+(1201)=362(辆),
故答案为:362;
(2)(120+18)(12012)=30(辆);
故答案为:30;
(3)6-3-1+18-7+5-12=6(辆),
∴该厂工人这一周超额完成任务6辆,
∴工资总额为:60×840+75×6=50850(元),
答:该厂工人这一周的工资总额是50850元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C,作直线BC,点P是抛物线上一个动点(点P不与点B,C重合),连结PB,PC,以PB,PC为边作CPBD,设CPBD的面积为S,点P的横坐标为m.
(1)求抛物线对应的函数表达式;
(2)当点P在第四象限,且CPBD有两个顶点在x轴上时,求点P的坐标;
(3)求S与m之间的函数关系式;
(4)当x轴将CPBD的面积分成1:7两部分时,直接写出m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式组:
(1)
 ;
;(2)
 ;
;(3)
 ;
;(4)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=30°,边AB的垂直平分线分别交AB和BC于点D,E,且AE平分∠BAC.
(1)求∠C的度数;
(2)若CE=1,求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=12,点C,D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,下列说法中正确的有( )
①△EFP的外接圆的圆心为点G;②四边形AEFB的面积不变;
③EF的中点G移动的路径长为4;④△EFP的面积的最小值为8.

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,如
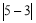 表示
表示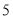 、
、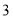 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;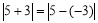 ,所以
,所以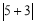 表示
表示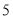 、
、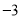 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离; ,所以
,所以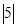 表示
表示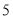 在数轴上对应的点到原点的距离.
在数轴上对应的点到原点的距离.一般地,点
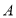 、点
、点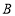 在数轴上分别表示有理数
在数轴上分别表示有理数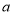 、
、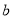 ,那么点
,那么点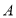 、点
、点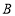 之间的距离可表示为
之间的距离可表示为 .
.(1)点
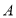 、
、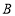 、
、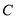 在数轴上分别表示有理数
在数轴上分别表示有理数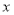 、
、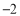 、
、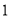 ,那么点
,那么点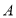 到点
到点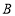 的距离与点
的距离与点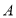 到点
到点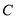 的距离之和可表示为__________(用含绝对值的式子表示).
的距离之和可表示为__________(用含绝对值的式子表示).(2)利用数轴探究:
①满足
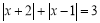 的
的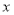 的取值范围是__________.
的取值范围是__________.②满足
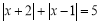 的
的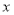 的所有值是__________.
的所有值是__________.③设
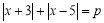 ,当
,当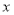 的值取在不小于
的值取在不小于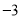 且不大于
且不大于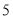 的范围时,
的范围时,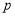 的值是不变的,而且是
的值是不变的,而且是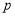 的最小值,这个最小值是_____.
的最小值,这个最小值是_____.(3)拓展:
①
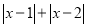 的最小值为__________.
的最小值为__________.②
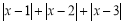 的最小值为__________.
的最小值为__________.③
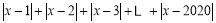 的最小值为__________,此时
的最小值为__________,此时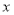 的取值范围为__________.
的取值范围为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.

相关试题

