【题目】如图,已知抛物线![]() 与直线
与直线![]() 交于点O(0,0),
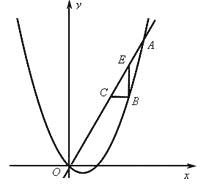
交于点O(0,0),![]() 。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。
。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。
(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造条形BCDE,设点D的坐标为(m,n),求m,n之间的关系式。
参考答案:
【答案】解:(1)∵点![]() 在直线
在直线![]() 上,∴
上,∴![]() ,即
,即![]() 。
。
∴点A的坐标是(6,12)。
又∵点A(6,12)在抛物线![]() 上,
上,
∴把A(6,12)代入![]() ,得
,得![]() 。
。
∴抛物线的函数解析式为![]() 。
。
(2)∵点C为OA的中点,∴点C的坐标是(3,6)。
把![]() 代入
代入![]() ,解得
,解得![]() (舍去)。
(舍去)。
∴![]() 。
。
(3)∵点D的坐标为(m,n),∴点E的坐标为![]() ,点C的坐标为
,点C的坐标为![]() 。
。
∴点B的坐标为![]() 。
。
把![]() 代入
代入![]() ,得
,得![]() ,即
,即![]() 。
。
∴m,n之间的关系式为![]() 。
。
【解析】
(1)根据点在曲线上,点的坐标满足于方程的关系,先求得由点A在直线![]() 上求得点A的坐标,再由点A在抛物线
上求得点A的坐标,再由点A在抛物线![]() 上,求得
上,求得![]() ,从而得到抛物线的函数解析式。
,从而得到抛物线的函数解析式。
(2)由于点B,C的纵坐标相等,从而由点C为OA的中点求得点C的坐标,将其纵坐标代入![]() ,求得
,求得![]() ,即可得到BC的长。
,即可得到BC的长。
(3)根据题意求出点B的坐标,代入![]() 即可求得m,n之间的关系式。
即可求得m,n之间的关系式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】开口向下的抛物线y=a(x+1)(x-9)与x轴交于A、B两点,与y轴交于点C,若∠ACB=90°,则a的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把抛物线y=
 x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为 ▲ .
x2交于点Q,则图中阴影部分的面积为 ▲ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过一次函数y=-
 x+3的图象与x轴、y轴的交点,并且也经过(1,1)点,求这个二次函数的关系式,并求x为何值时,函数有最大(最小)值?这个值是多少?
x+3的图象与x轴、y轴的交点,并且也经过(1,1)点,求这个二次函数的关系式,并求x为何值时,函数有最大(最小)值?这个值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
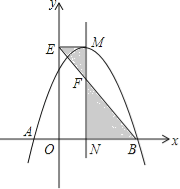
 与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).(1)求该抛物线的解析式及顶点M的坐标;
(2)求△EMF与△BNF的面积之比.
-
科目: 来源: 题型:
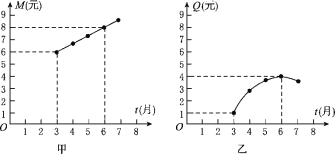
查看答案和解析>>【题目】某公司为指导某种应季商品的生产和销售,对三月份至七月份该商品的售价和成本进行了调研,结果如下:一件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图甲),一件商品的成本Q(元)与时间t(月)的关系可用一段抛物线上的点来表示,其中6月份成本最高(如图乙).根据图象提供的信息解答下面的问题:
(1)一件商品在3月份出售时的利润是多少元?(利润=售价-成本)
(2)求出一件商品的成本Q(元)与时间t(月)之间的函数关系式;
(3)你能求出3月份至7月份一件商品的利润W(元)与时间t(月)之间的函数关系式吗?若该公司能在一个月内售出此种商品30 000件,请你计算该公司在一个月内最少获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式,并写出y<0时,对应x的取值范围;
(2)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.
①当BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a,b),将矩形ABCD的周长L表示为a的函数并写出自变量的取值范围,判断周长是否存在最大值?如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
相关试题

