【题目】如图,在正方形ABCD中,点E、F分别为DC、BC边上的点,且∠EAF=45°,若将△ADE绕点A顺时针方向旋转90°得到△ABG.回答下列问题:
(1)∠GAF等于多少度?为什么?
(2)EF与FG相等吗?为什么?
(3)△AEF与△AGF有何种位置关系?

参考答案:
【答案】解:(1)∠GAF=45°;(2)EF=FG;(3)△AEF与△AGF关于直线AF轴对称.
【解析】
(1)由旋转的性质可知△ADE≌△ABG,可知AE=AG,∠DAE=∠BAG,故∠GAF=∠GAB+∠BAF=∠DAE+∠BAF=∠BAD-∠EAF;
(2)由(1)可知∠EAF=∠GAF,且AE=AG,AF=AF,可证△AEF≌△AGF,从而得EF=FG;
(3)根据(2)可知△AEF≌△AGF.
解:(1)∠GAF=45°.
∵△ABG是将△ADE绕A点顺时针旋转90°得到的,
∴∠DAE=∠BAG,
∵∠EAF=45°,∠BAD=90°,
∴∠DAE+∠FAB=90°﹣45°=45°,
∴∠BAG+∠FAB=45°,即∠GAF=45°;
(2)EF=FG.
理由:∵△ABG是△ADE旋转90°得到的,
∴AE=AG,
∵∠EAF=45°,∠GAF=45°,
∴∠EAF=∠GAF,
在△AEF和△AGF中,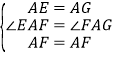 ,
,
∴△AEF≌△AGF,
∴EF=FG;
(3)△AEF与△AGF关于直线AF轴对称.
由△AEF≌△AGF易证.
-
科目: 来源: 题型:
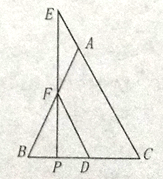
查看答案和解析>>【题目】如图,在ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为P,EP交AB于点F,FD∥AC交BC于点D.求证:△AEF是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的坐标系中,△ABC的三个顶点的坐标依次为A(﹣1,2),B(﹣4,1),C(﹣2,﹣2).
(1)请在这个坐标系中作出△ABC关于y轴对称的△A1B1C1.
(2)分别写出点A1、B1、C1的坐标.
(3)求△A1B1C1的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】母亲节前夕,某淘宝店主从厂家购进A、B两种礼盒,已知A、B两种礼盒的单价比为2:3,单价和为200元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该店主购进这两种礼盒恰好用去9600元,且购进A种礼盒最多36个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)根据市场行情,销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元.为奉献爱心,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,m值是多少?此时店主获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是( )

A.30°
B.45°
C.60°
D.40° -
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种新运算“a☆b”的含义为:当a≥b时,a☆b=a+b;当a<b时,a☆b=a-b.例如:3☆(-4)=3+(-4)=-1,(-6)☆
 =-6-
=-6- =-6
=-6 .
.(1)填空:(-4)☆3=______;
(2)如果(3x-4)☆(2x+8)=(3x-4)-(2x+8),求x的取值范围;
(3)如果(3x-7)☆(3-2x)=2,求x的值.
相关试题

