【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t(s).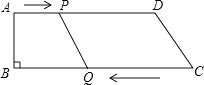
(1)当t为何值时,PQ∥CD?
(2)当t为何值时,PQ=CD?
参考答案:
【答案】
(1)解:根据题意得:PA=t,CQ=3t,则PD=AD﹣PA=24﹣t.
∵AD∥BC,
即PD∥CQ,
∴当PD=CQ时,四边形PQCD为平行四边形,
即24﹣t=3t,
解得:t=6,
即当t=6时,PQ∥CD;
(2)解:若PQ=DC,分两种情况:
①PD=QC,由(1)可知,t=6,
②PD≠CQ,则四边形PDCQ是等腰梯形,则有QC=PD+2(BC﹣AD),
可得方程:3t=24﹣t+4,
解得:t=7.
【解析】(1)根据题意得:PA=t,CQ=3t,则PD=AD﹣PA=24﹣t.根据一组对边平行且相等得四边形是平行四边形得出方程,求解得出t的值,然后根据平行四边形的性质定理得出结论;
(2)若PQ=DC,分两种情况:①PQ=DC,由(1)可知,t=6,②PD≠CQ,则四边形PDCQ是等腰梯形,则有QC=PD+2(BC﹣AD),得出方程求解即可。
【考点精析】关于本题考查的平行四边形的判定与性质和直角梯形,需要了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;一腰垂直于底的梯形是直角梯形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段
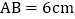 ,动点
,动点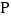 以
以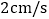 的速度从
的速度从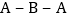 在线段
在线段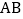 上运动,到达点
上运动,到达点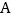 后,停止运动;动点
后,停止运动;动点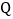 以
以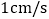 的速度从
的速度从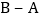 在线段
在线段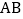 上运动,到达点
上运动,到达点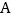 后,停止运动.若动点
后,停止运动.若动点 同时出发,设点
同时出发,设点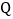 的运动时间是
的运动时间是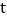 (单位:
(单位: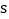 )时,两个动点之间的距离为S(单位:
)时,两个动点之间的距离为S(单位: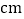 ),则能表示
),则能表示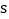 与
与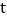 的函数关系的是( )
的函数关系的是( )
A.
 B.
B. 
C.
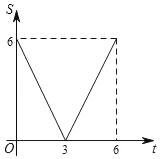 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,
求证:AE2+AD2=2AC2 .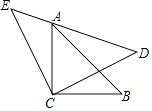
-
科目: 来源: 题型:
查看答案和解析>>【题目】韦魏一家三口随旅游团去九寨沟旅游,王聪把旅途费用支出情况制成了如下的统计图:
(1)哪一部分的费用占整个支出的
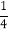 ?
?(2)若他们共花费人民币8600元,则在食宿上用去多少元?
(3)这一家住返的路费共多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各顶点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出A′、B′、C′的坐标,并在图中画出平移后图形;
(3)求出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.求证:

(1)AB∥CD;
(2)∠2+∠3=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠BAC=20°,∠ACF=80°.
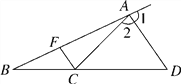
(1)求∠2的度数;
(2)FC与AD平行吗?为什么?
(3)根据以上结论,你能确定∠ADB与∠FCB的大小关系吗?请说明理由.
相关试题

