【题目】如图,已知∠1=∠2,∠BAC=20°,∠ACF=80°.
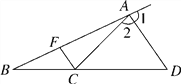
(1)求∠2的度数;
(2)FC与AD平行吗?为什么?
(3)根据以上结论,你能确定∠ADB与∠FCB的大小关系吗?请说明理由.
参考答案:
【答案】(1) ∠2=80°;(2)答案见解析;(3) 答案见解析.
【解析】试题分析:(1)利用平角定义,根据题意确定出∠2的度数即可;
(2)FC与AD平行,理由为:利用内错角相等两直线平行即可得证;
(3)∠ADB=∠FCB,理由为:由FC与AD平行,利用两直线平行同位角相等即可得证.
试题解析:(1)∵∠1=∠2,∠BAC=20°,∠1+∠2+∠BAC=180°,
∴∠2=80°;
(2)∵∠2=∠ACF=80°,
∴FC∥AD;
(3)∠ADB=∠FCB,理由为:
证明:∵FC∥AD,
∴∠ADB=∠FCB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t(s).
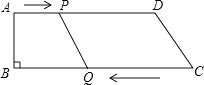
(1)当t为何值时,PQ∥CD?
(2)当t为何值时,PQ=CD? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各顶点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出A′、B′、C′的坐标,并在图中画出平移后图形;
(3)求出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.求证:

(1)AB∥CD;
(2)∠2+∠3=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为
A(﹣1,1),B(﹣3,1),C(﹣1,4).
①画出△ABC关于y轴对称的△A1B1C1;
②将△ABC绕着点B顺时针旋转90°后得到△A2BC2 , 请在图中画出△A2BC2 , 并求出线段BC旋转过程中所扫过的面积(结果保留π).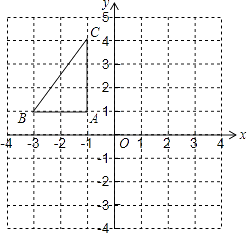
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;比如我们通过学习特殊的四边形,即平行四边形(继续学习它们的特殊类型如矩形、菱形等)来逐步认识四边形;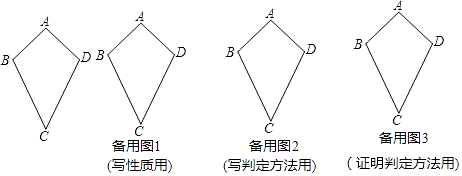
我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;
请解决以下问题:
如图,我们把满足AB=AD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”;
(1)写出筝形的两个性质(定义除外);
(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A的坐标为(4,﹣3),且OA=5,在x轴上确定一点P,使△AOP为等腰三角形.
(1)写出一个符合题意的点P的坐标 ;
(2)请在图中画出所有符合条件的△AOP.

相关试题

