【题目】如图,PA为⊙O的切线,A为切点.过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E.
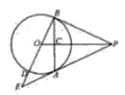
(1)求证:PB为⊙O的切线;(2)若tan∠ABE=![]() ,求sinE的值.
,求sinE的值.
参考答案:
【答案】
(1)证明:连接OA
∵PA为⊙O的切线,
∴∠PAO=90°
∵OA=OB,OP⊥AB于C
∴BC=CA,PB=PA
∴△PBO≌△PAO
∴∠PBO=∠PAO=90°
∴PB为⊙O的切线
(2)解法1:连接AD,∵BD是直径,∠BAD=90°
由(1)知∠BCO=90°
∴AD∥OP
∴△ADE∽△POE
∴EA/EP=AD/OP 由AD∥OC得AD=2OC ∵tan∠ABE="1/2 " ∴OC/BC=1/2,设OC=t,则BC=2t,AD=2t由△PBC∽△BOC,得PC=2BC=4t,OP=5t
∴EA/EP=AD/OP=2/5,可设EA=2m,EP=5m,则PA=3m
∵PA=PB∴PB=3m
∴sinE=PB/EP=3/5
(2)解法2:连接AD,则∠BAD=90°由(1)知∠BCO=90°∵由AD∥OC,∴AD=2OC ∵tan∠ABE=1/2,∴OC/BC=1/2,设OC=t,BC=2t,AB=4t由△PBC∽△BOC,得PC=2BC=4t,
∴PA=PB=2![]() t 过A作AF⊥PB于F,则AF·PB=AB·PC
t 过A作AF⊥PB于F,则AF·PB=AB·PC
∴AF=![]() t 进而由勾股定理得PF=
t 进而由勾股定理得PF=![]() t
t
∴sinE=sin∠FAP=PF/PA=3/5
【解析】略
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣a3)2的结果是( )
A.﹣a5
B.a5
C.a6
D.﹣a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BD交AD于点E.已知AB=2,△DOE的面积为
 ,则AE的长为( )
,则AE的长为( ) 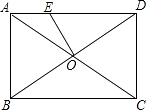
A.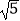
B.2
C.1.5
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是x2﹣3x+1=0的根,则2a2﹣6a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班7名女生的体重(单位:kg)分别是35、37、38、40、42、42、74,这组数据的众数是( )
A. 74B. 44C. 42D. 40
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A.2
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m是方程2x2﹣3x=1的一个根,则6m2﹣9m的值为_____.
相关试题

