【题目】为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了3.2米(BB‘),再把竹竿竖立在地面上,测得竹竿的影长(B‘C‘)为1.8米,求路灯离地面的高度.
参考答案:
【答案】![]()
【解析】试题分析:先根据AB⊥OC′,OS⊥OC′可知△ABC∽△SOC,同理可得△A′B′C′∽△SOC′,再由相似三角形的对应边成比例即可得出h的值.
试题解析:∵AB⊥OC′,OS⊥OC′,
∴SO∥AB,
∴△ABC∽△SOC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得OB=![]() h﹣1①,
h﹣1①,
同理,∵A′B′⊥OC′,
∴△A′B′C′∽△SOC′,
∴![]() =
=![]() ,
,![]() =
=![]() ②,
②,
把①代入②得,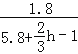 =
=![]() ,
,
解得h=9(米).
答:路灯离地面的高度是9米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2-2mx+m2-1.

(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;
(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;
(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC于E,若线段AE=5,则S四边形ABCD=

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从
A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒.

(1)用含t的代数式表示P到点A和点C的距离:PA=________,PC=_____________
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,当点P运动到点C时,P、Q两点运动停止,
①当P、Q两点运动停止时,求点P和点Q的距离;
②求当t为何值时P、Q两点恰好在途中相遇。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=k1x+b 与反比例函数
 的图象交于点A(2,m)和B(﹣6,﹣2),与y轴交于点C.
的图象交于点A(2,m)和B(﹣6,﹣2),与y轴交于点C.(1)y1=___,y2= ;
(2)根据函数图象可知,当 y1<y2时,x的取值范围是 ;
(3)过点A作AD⊥x轴于点D,求△ABD的面积.
(4)点P是反比例函数图象上一点,△POD的面积是5,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线y=﹣2x+4与两坐标轴分别交于点A、B,点C为线段OA上一动点,连接BC,作BC的中垂线分别交OB、AB交于点D、E.

(l)当点C与点O重合时,DE= ;
(2)当CE∥OB时,证明此时四边形BDCE为菱形;
(3)在点C的运动过程中,直接写出OD的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把菱形
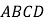 沿
沿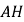 折叠,
折叠,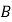 落在
落在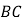 边上的
边上的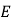 处,若
处,若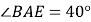 ,则
,则 的大小为( )
的大小为( )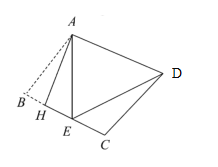
A.
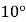 B.
B.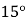 C.
C.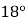 D.
D.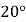
相关试题

