【题目】在一个不透明的袋子中,装有除颜色外其余均相同的红、蓝两种球,已知其中红球有3个,且从中任意摸出一个是红球的概率为0.75.
(1)根据题意,袋中有 个蓝球.
(2)若第一次随机摸出一球,不放回,再随机摸出第二个球.请用画树状图或列表法求“摸到两球中至少一个球为蓝球(记为事件A)”的概率P(A).
参考答案:
【答案】(1)1;(2) ![]()
【解析】试题分析:根据红球的个数和红球的概率可求出总球的个数,然后相减即可;
(2)根据题意画出树状图,然后求出总可能数和符合条件的次数,根据概率公式求解即可.
试题解析:(1)1.
(2)将袋中各球分别记为红1、红2、红3、蓝.根据题意,可以画出如下的树状图:

由树状图可以看出,所有可能出现的结果共有12种,这些结果出现的可能性相等,其中事件A的结果共有6种,所以 P(A)= ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程(2x﹣1)(3x+1)=x2+2化为一般形式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.
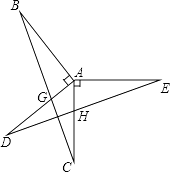
求证:
(1)△ABC≌△ADE;
(2)BC⊥DE. -
科目: 来源: 题型:
查看答案和解析>>【题目】为寻求合适的销售价格,商场对新进的一种商品进行了一周的试销,发现这种商品的每天销售量y(千克)与销售价格x(元/千克)之间成反比例关系.已知第一天以220元/千克的价格销售了80千克.
(1)求y与x的函数关系式.
(2)试销期间共销售了700千克这种新进商品,在试销后,商场决定将这种新进商品的销售价格定为160元/千克,这样按所发现的反比例关系预测剩余这种商品再用10天可以全部售完.问商场共新进多少千克的这种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画出数轴,把数3,﹣3.5,0,
 ,
,  ,+4在数轴上表示出来,并用“<”把它们连接起来.
,+4在数轴上表示出来,并用“<”把它们连接起来. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
相关试题

