【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
参考答案:
【答案】(1)每吨水的政府补贴优惠价2元,市场调节价为3.5元;(2)![]() ;(3)69.
;(3)69.
【解析】
试题分析:(1)设每吨水的政府补贴优惠价为m元,市场调节价为n元,根据题意列出方程组,求解此方程组即可;
(2)根据用水量分别求出在两个不同的范围内y与x之间的函数关系,注意自变量的取值范围;
(3)根据小英家5月份用水26吨,判断其在哪个范围内,代入相应的函数关系式求值即可.
试题解析:(1)设每吨水的政府补贴优惠价为m元,市场调节价为n元.![]() ,解得:
,解得:![]() .
.
答:每吨水的政府补贴优惠价2元,市场调节价为3.5元.
(2)当0≤x≤14时,y=2x;
当x>14时,y=14×2+(x﹣14)×3.5=3.5x﹣21,故所求函数关系式为:![]() ;
;
(3)∵26>14,∴小英家5月份水费为3.5×26﹣21=69元.
答:小英家5月份水费69元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】与点P(5,-3)关于x 轴对称的点的坐标是( )
A.(5,3)
B.(-5,3)
C.(-3,5)
D.(3,-5) -
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车收费标准是:起步价为8元,3千米后每千米为2元,若某人乘坐了x(x>5)千米.
(1)用含x的代数式表示他应支付的车费.
(2)行驶30千米,应付多少钱?
(3)若他支付了46元,你能算出他乘坐的路程吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
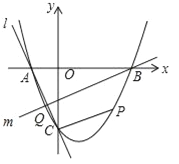
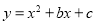 与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知矩形ABED(两组对边分别相等,四个内角都是直角),点C是边DE的中点,且AB=2AD.
(1)判断△ABC的形状,并说明理由;
(2)保持图1中△ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.
 2
2 -
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明命题:“四边形中至少有一个角是钝角或直角”时,首先应该假设这个四边形中( )
A.有一个角是钝角或直角B.每一个角都是钝角
C.每一个角都是直角D.每一个角都是锐角
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班55名学生在2018年(下)期末的县质量检测中,数学成绩在90~110分这个分数段的频率为0.2,则该班在这个分数段的学生有_____人.
相关试题

