搜索
【题目】完成下面的说理过程．
已知：如图，OA＝OB，AC＝BC.
试说明：∠AOC＝∠BOC.
解：在△AOC和△BOC中，
因为OA＝______，AC＝______，OC＝______，
所以________≌________(SSS)，
所以∠AOC＝∠BOC(__________________)．
参考答案：
【答案】OB；BC；OC；△AOC；△BOC；全等三角形的对应角相等.
【解析】
解得本题,根据已知条件OA=OB,AC=BC以及所隐含条件OC为公共边,可以证明△AOC≌△BOC, 根据全等三角形的性质即可得∠AOC=∠BOC.
证明: 在△AOC和△BOC中,
,
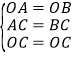△AOC≌△BOC (SSS).
∠AOC=∠BOC (全等三角形的对应角相等).
故答案为:
OB;BC;OC;△AOC;△BOC; 全等三角形的对应角相等.
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合题。
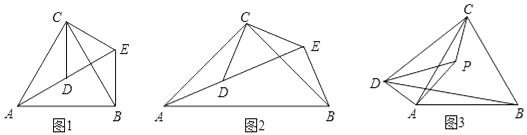
（1）问题发现：如图1，△ACB和△DCE均为等边三角形，当△DCE旋转至点A，D，E在同一直线上，连接BE，易证△BCE≌△ACD．则
①∠BEC=°；②线段AD、BE之间的数量关系是 ．
（2）拓展研究：
如图2，△ACB和△DCE均为等腰三角形，且∠ACB=∠DCE=90°，点A、D、E在同一直线上，若AE=15，DE=7，求AB的长度．
（3）探究发现：
如图3，P为等边△ABC内一点，且∠APC=150°，且∠APD=30°，AP=5，CP=4，DP=8，求BD的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连接BF、CE，且∠FBD=35°，∠BDF=75°，下列说法：①△BDF≌CDE；②ABD和△ACD面积相等；③BF∥CE；④∠DEC=70°，其中正确的有（ ）
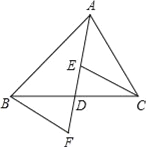
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图1，直线y=
x+6与x轴、y轴分别交于点A、C两点，点B的横坐标为2．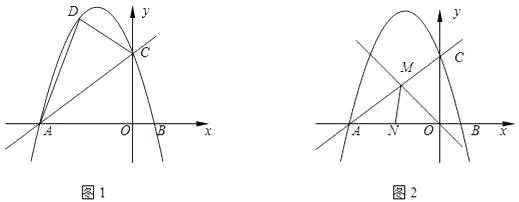 
（1）求A、C两点的坐标和抛物线的函数关系式；
（2）点D是直线AC上方抛物线上任意一点，P为线段AC上一点，且S△PCD=2S△PAD ， 求点P的坐标；
（3）如图2，另有一条直线y=﹣x与直线AC交于点M，N为线段OA上一点，∠AMN=∠AOM．点Q为x轴负半轴上一点，且点Q到直线MN和直线MO的距离相等，求点Q的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知CE⊥AB于点E，BD⊥AC于点D，BD与CE交于点O，且AO平分∠BAC.
(1)图中有多少对全等三角形？请你一一列举出来(不要求说明理由)．
(2)小明说：欲说明BE＝CD，可先说明△AOE≌△AOD得到AE＝AD，再说明△ADB≌△AEC得到AB＝AC，然后利用等式的性质即可得到BE＝CD，请问他的说法正确吗？如果不正确，请说明理由；如果正确，请按他的思路写出推导过程．
(3)要得到BE＝CD，你还有其他的思路吗？请仿照小明的说法具体说一说你的想法．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知下面三组数值：①
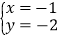②
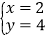③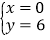
其中是方程组
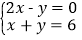的解的是( )A. ① B. ② C. ③ D. 都不是
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果a=（-99）0 ， b=（-0.1）-1 ， c=（-
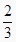）-2 ， 那么a ， b ， c三数的大小为（ ）
A.a＞b＞c
B.c＞a＞b
C.a＞c＞b
D.c＞b＞a
相关试题
