搜索
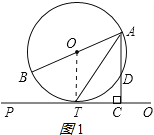
【题目】如图，AB为⊙O的直径，D、T是圆上的两点，且AT平分∠BAD，过点T作AD的延长线的垂线PQ，垂足为C．
（1）求证：PQ是⊙O的切线；
（2）已知⊙O的半径为2，若过点O作OE⊥AD，垂足为E，OE=
，求弦AD的长．
参考答案：
【答案】（1）见解析；（2）AD=2
【解析】
试题分析：连接OT，根据OA=OT得出∠OAT=∠OTA，根据AT为角平分线得出∠OAT=∠CAT，从而得出OT∥AC，根据PQ⊥AC得出切线；根据垂径定理得出答案．
试题解析：（1）证明：连接OT，如图1所示： ∵OA=OT， ∴∠OAT=∠OTA， ∵AT平分∠BAD，
∴∠OAT=∠CAT， ∴∠OTA=∠CAT， ∴OT∥AC， ∵PQ⊥AC， ∴PQ⊥OT， ∴PQ是⊙O的切线；
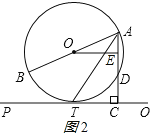
（2）解：如图2所示： ∵OE⊥AD， ∴AE=DE，∠AEO=90°，
∴AE=
=
=1， ∴AD=2AE=2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，且AB =6，C是⊙O上一点，D是
的中点，过点D作⊙O的切线，与AB、AC的延长线分别交于点E、F，连接AD.
(l)求证：AF⊥EF;
(2)填空：
①当BE= 时，点C是AF的中点；
②当BE= 时，四边形OBDC是菱形，
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB＝AC，以AB为直径的⊙O交AC边于点D，过点C作CF∥AB，与过点B的切线交于点F，连接BD.
(1)求证：BD＝BF；
(2)若AB＝10，CD＝4，求BC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将某中学九年级组的全体教师按年龄分成三组，情况如下表所示，则表中a的值是_________.
第一组
第二组
第三组
频数
6
10
a
频率
b
c
0.2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，CD是⊙O的直径，且CD=2cm，点P为CD的延长线上一点，过点P作⊙O的切线PA，PB，切点分别为点A，B．
（1）连接AC，若∠APO=30°，试证明△ACP是等腰三角形；
（2）填空：
①当DP= cm时，四边形AOBD是菱形；
②当DP= cm时，四边形AOBP是正方形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB，BC，CD分别与⊙O相切于E，F，G．且AB∥CD．BO=6cm，CO=8cm．
（1）求证：BO⊥CO；
（2）求BE和CG的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列计算正确的是（ ）
A.3x2y一2x2y=x2y
B.5y一3y=2
C.3a+2b=5ab
D.7a+a=7a2
相关试题
