【题目】如图,弦BE与弦CD交于点G,点E为 ![]() 的中点,过点B的直线交DC延长线于点A,AB∥DE.
的中点,过点B的直线交DC延长线于点A,AB∥DE.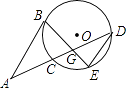
(1)若AB=AG,求证:AB是⊙O切线;
(2)在(1)条件下,若tanA= ![]() ,DE=10,求⊙O的半径.
,DE=10,求⊙O的半径.
(3)求证:AG2﹣BG2=ACAG.
参考答案:
【答案】
(1)证明:如图1中,连接OB、OE交AD于F.
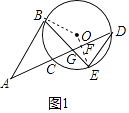
∵ ![]() =
= ![]() ,
,
∴OE⊥CD,
∴∠EFG=90°,
∴∠GEF+∠EGF=90°,
∵AB=AG,
∴∠ABG=∠AGB=∠EGF,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠ABG+∠OBE=90°,
∴∠ABO=90°
∴AB是⊙O的切线.
(2)解:如图2中,连接OD.
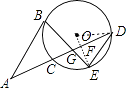
∵AB∥DE,
∴∠A=∠ADE,
在Rt△DFE中,tan∠DFE= ![]() =
= ![]() ,设EF=3k,DF=4k,则DE=5k,
,设EF=3k,DF=4k,则DE=5k,
由题意DE=10,
∴5k=10,
∴k=2,
∴EF=6,DF=8,
设⊙O的半径为r,
在Rt△ODF中,∵OD2=OF2+DF2,
∴r2=(r﹣6)2+82,
∴r= ![]() .
.
(3)证明:如图3中,连接BC.
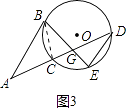
∵AB∥DE,
∴∠A=∠ADE,
∵∠CBG=∠ADE,
∴∠CBG=∠A,∵∠BGC=∠AGB,
∴△BGC∽△AGB,
∴ ![]() =
= ![]() ,
,
∴BG2=AGCG,
∴AG2﹣BG2=AG2﹣AGCG=AG(AG﹣CG)=AGAC.
【解析】(1)连接OB、OE交AD于F.首先依据垂径定理的推理可得到∠EFG=90°,则∠GEF+∠EGF=90°,接下来,再证明∠ABG=∠EGF,∠OBE=∠OEB,依据等式的性质可证明∠ABG+∠OBE=90°,最后依据切线的判定定理进行证明即可;
(2)连接OD.在Rt△DFE中,设EF=3k,DF=4k,依据勾股定理可知DE=5k,由题意DE=10,可得k=2,推出EF=6,DF=8,设⊙O的半径为r,在Rt△ODF中,根据OD2=OF2+DF2列出关于r的方程求解即可;
(3)连接BC.首先证明△BGC∽△AGB,依据相似三角形的性质可得到BG2=AGCG,将BG2=AGCG代入变形即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张两边分别平行的纸条折成如图所示,EF为折痕,ED交BF于点G,且∠EFB=48°,则下列结论: ①∠DEF=48°;②∠AED=84°;③∠BFC=84°;④∠DGF=96°,其中正确的个数有( )
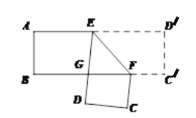
A. 4个B. 3个C. 2个D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D.

(1)求证:△ACB∽△ADE;
(2)求AD的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(2,﹣2),B(6,﹣2),动点P从点O出发,沿着x轴正方向以每秒2个单位的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<4).△OPQ与四边形OABC重叠部分的面积为S.
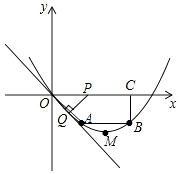
(1)求经过O、A、B三点的抛物线的解析式;
(2)若将△OPQ沿着直线PQ翻折得到△O′PQ,则当t=时,点O′恰好在抛物线上.
(3)在(2)的条件下,记△O′PQ与四边形OABC重叠的面积为S,求S与t的函数关系式,并注明自变量的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将直角三角形ACB,
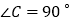 ,AC=6,沿CB方向平移得直角三角形DEF,BF=2,DG=
,AC=6,沿CB方向平移得直角三角形DEF,BF=2,DG= ,阴影部分面积为_______.
,阴影部分面积为_______.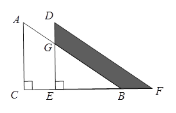
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,点P为边BC上一点,在AC上取一点D,使AD=AP.
(1)若∠APD=80°,求∠DPC的度数;
(2)若∠APD=α,求∠BAP(用含α的式子表示).
相关试题

