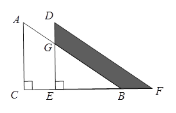
【题目】如图所示,将直角三角形ACB, ![]() ,AC=6,沿CB方向平移得直角三角形DEF,BF=2,DG=
,AC=6,沿CB方向平移得直角三角形DEF,BF=2,DG=![]() ,阴影部分面积为_______.
,阴影部分面积为_______.
参考答案:
【答案】10.5
【解析】
根据平移的性质,对应点间的距离等于平移的距离求出CE=BF,再求出GE,然后根据平移变换只改变图形的位置不改变图形的形状与大小可得△ABC的面积等于△DEF的面积,从而得到阴影部分的面积等于梯形ACEG的面积,再利用梯形的面积公式列式计算即可得解.
∵△ACB平移得到△DEF,∴CE=BF=2,DE=AC=6,∴GE=DE﹣DG=6![]() 4.5,由平移的性质,S△ABC=S△DEF,∴阴影部分的面积=S梯形ACEG
4.5,由平移的性质,S△ABC=S△DEF,∴阴影部分的面积=S梯形ACEG![]() (GE+AC)CE
(GE+AC)CE![]() (4.5+6)×2=10.5.
(4.5+6)×2=10.5.
故答案为:10.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D.

(1)求证:△ACB∽△ADE;
(2)求AD的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,弦BE与弦CD交于点G,点E为
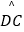 的中点,过点B的直线交DC延长线于点A,AB∥DE.
的中点,过点B的直线交DC延长线于点A,AB∥DE.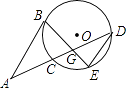
(1)若AB=AG,求证:AB是⊙O切线;
(2)在(1)条件下,若tanA= ,DE=10,求⊙O的半径.
,DE=10,求⊙O的半径.
(3)求证:AG2﹣BG2=ACAG. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(2,﹣2),B(6,﹣2),动点P从点O出发,沿着x轴正方向以每秒2个单位的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<4).△OPQ与四边形OABC重叠部分的面积为S.
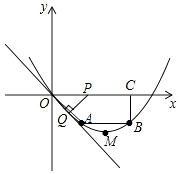
(1)求经过O、A、B三点的抛物线的解析式;
(2)若将△OPQ沿着直线PQ翻折得到△O′PQ,则当t=时,点O′恰好在抛物线上.
(3)在(2)的条件下,记△O′PQ与四边形OABC重叠的面积为S,求S与t的函数关系式,并注明自变量的取值范围. -
科目: 来源: 题型:
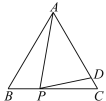
查看答案和解析>>【题目】如图,△ABC为等边三角形,点P为边BC上一点,在AC上取一点D,使AD=AP.
(1)若∠APD=80°,求∠DPC的度数;
(2)若∠APD=α,求∠BAP(用含α的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列手机软件图标中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
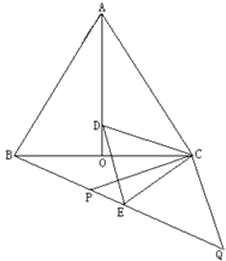
查看答案和解析>>【题目】如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE;
(2)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=5,若BC=8时,求PQ的长.
相关试题