【题目】解决问题:
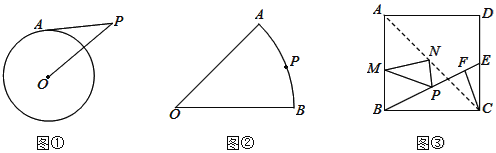
![]() 如图
如图![]() ,半径为4的
,半径为4的![]() 外有一点P,且
外有一点P,且![]() ,点A在
,点A在![]() 上,则PA的最大值和最小值分别是______和______.
上,则PA的最大值和最小值分别是______和______.
![]() 如图
如图![]() ,扇形AOB的半径为4,
,扇形AOB的半径为4,![]() ,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得
,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得![]() 周长的最小,请在图
周长的最小,请在图![]() 中确定点E、F的位置并直接写出
中确定点E、F的位置并直接写出![]() 周长的最小值;
周长的最小值;
拓展应用
![]() 如图
如图![]() ,正方形ABCD的边长为
,正方形ABCD的边长为![]() ;E是CD上一点
;E是CD上一点![]() 不与D、C重合
不与D、C重合![]() ,
,![]() 于F,P在BE上,且
于F,P在BE上,且![]() ,M、N分别是AB、AC上动点,求
,M、N分别是AB、AC上动点,求![]() 周长的最小值.
周长的最小值.
参考答案:
【答案】(1)11,3;(2)图见解析,![]() 周长最小值为
周长最小值为![]() ;(3)
;(3)![]() .
.
【解析】
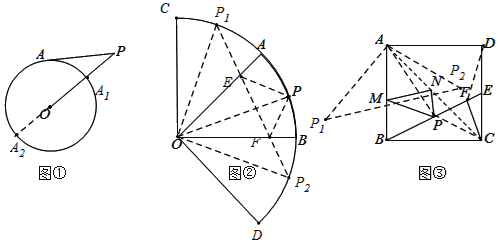
![]() 根据圆外一点P到这个圆上所有点的距离中,最远是和最近的点是过圆心和该点的直线与圆的交点,容易求出最大值与最小值分别为11和3;
根据圆外一点P到这个圆上所有点的距离中,最远是和最近的点是过圆心和该点的直线与圆的交点,容易求出最大值与最小值分别为11和3;
![]() 作点P关于直线OA的对称点
作点P关于直线OA的对称点![]() ,作点P关于直线OB的对称点
,作点P关于直线OB的对称点![]() ,连接
,连接![]() 、
、![]() ,与OA、OB分别交于点E、F,点E、F即为所求,此时
,与OA、OB分别交于点E、F,点E、F即为所求,此时![]() 周长最小,然后根据等腰直角三角形求解即可;
周长最小,然后根据等腰直角三角形求解即可;
![]() 类似
类似![]() 题作对称点,
题作对称点,![]() 周长最小
周长最小![]() ,然后由三角形相似和勾股定理求解.
,然后由三角形相似和勾股定理求解.
解:![]() 如图
如图![]() ,
,![]() 圆外一点P到这个圆上所有点的距离中,最大距离是和最小距离都在过圆心的直线OP上,
圆外一点P到这个圆上所有点的距离中,最大距离是和最小距离都在过圆心的直线OP上,
此直线与圆有两个交点,圆外一点与这两个交点的距离个分别最大距离和最小距离.
![]() 的最大值
的最大值![]() ,
,
PA的最小值![]() ,
,
故答案为11和3;
![]() 如图
如图![]() ,以O为圆心,OA为半径,画弧AB和弧BD,作点P关于直线OA的对称点
,以O为圆心,OA为半径,画弧AB和弧BD,作点P关于直线OA的对称点![]() ,作点P关于直线OB的对称点
,作点P关于直线OB的对称点![]() ,连接
,连接![]() 、
、![]() ,与OA、OB分别交于点E、F,点E、F即为所求.
,与OA、OB分别交于点E、F,点E、F即为所求.
连接![]() 、
、![]() 、OP、PE、PF,
、OP、PE、PF,
由对称知识可知,![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,
,
![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
![]() 周长
周长![]() ,此时
,此时![]() 周长最小.
周长最小.
故答案为![]() ;
;
![]() 作点P关于直线AB的对称
作点P关于直线AB的对称![]() ,连接
,连接![]() 、
、![]() ,作点P关于直线AC的对称
,作点P关于直线AC的对称![]() ,
,
连接![]() 、
、![]() ,与AB、AC分别交于点M、N.如图③
,与AB、AC分别交于点M、N.如图③
由对称知识可知,![]() ,
,![]() ,
,![]() 周长
周长![]() ,
,
此时,![]() 周长最小
周长最小![]() .
.
由对称性可知,![]() ,
,![]() ,
,![]() ,
,
∴![]()
![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() 周长最小值
周长最小值![]() ,当AP最短时,周长最小.
,当AP最短时,周长最小.
连接DF.
![]() ,且
,且![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,
![]() 在
在![]() 与
与![]() 中,
中,![]() ,
,![]()
![]() ∽
∽![]() ,
,
![]() ,
,
∴![]()
![]() ,取AB中点O.
,取AB中点O.
![]() 点F在以BC为直径的圆上运动,当D、F、O三点在同一直线上时,DF最短.
点F在以BC为直径的圆上运动,当D、F、O三点在同一直线上时,DF最短.
![]() ,
,
![]() 最小值为
最小值为![]()
![]() 此时,
此时,![]() 周长最小值
周长最小值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线
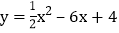 的顶点M在直线L:
的顶点M在直线L: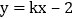 上.
上. 求直线L的函数表达式;
求直线L的函数表达式; 现将抛物线沿该直线L方向进行平移,平移后的抛物线的顶点为N,与x轴的右交点为C,连接NC,当
现将抛物线沿该直线L方向进行平移,平移后的抛物线的顶点为N,与x轴的右交点为C,连接NC,当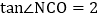 时,求平移后的抛物线的解析式.
时,求平移后的抛物线的解析式.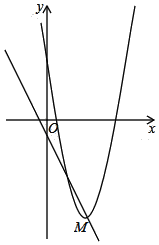
-
科目: 来源: 题型:
查看答案和解析>>【题目】“机动车行驶到斑马线要礼让行人”等交通法规实施后,某校数学课外实践小组就对这些交通法规的了解情况在全校随机调查了部分学生,调查结果分为四种:
 非常了解,
非常了解, 比较了解,
比较了解, 基本了解,
基本了解, 不太了解,实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图.
不太了解,实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图.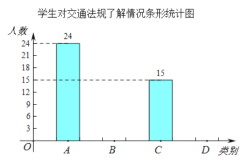

请结合图中所给信息解答下列问题:
 本次共调查______名学生;扇形统计图中C所对应扇形的圆心角度数是______;
本次共调查______名学生;扇形统计图中C所对应扇形的圆心角度数是______; 补全条形统计图;
补全条形统计图; 该校共有800名学生,根据以上信息,请你估计全校学生中对这些交通法规“非常了解”的有多少名?
该校共有800名学生,根据以上信息,请你估计全校学生中对这些交通法规“非常了解”的有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从一架水平飞行的无人机
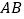 的尾端点
的尾端点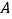 测得正前方的桥的左端点
测得正前方的桥的左端点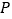 俯角为
俯角为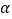 ,且
,且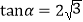 ,无人机的飞行高度
,无人机的飞行高度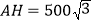 米,桥的长度
米,桥的长度 为1255米.
为1255米.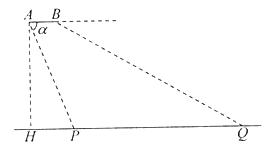
(1)求点
 到桥左端点
到桥左端点 的距离;
的距离;(2)若从无人机前端点
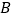 测得正前方的桥的右端点
测得正前方的桥的右端点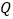 的俯角为
的俯角为 ,求这架无人机的长度
,求这架无人机的长度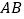 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
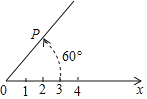
A. Q(3,240°) B. Q(3,﹣120°) C. Q(3,600°) D. Q(3,﹣500°)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆某中学组织七、八、九年级学生参加“直辖20年,点赞新重庆”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.
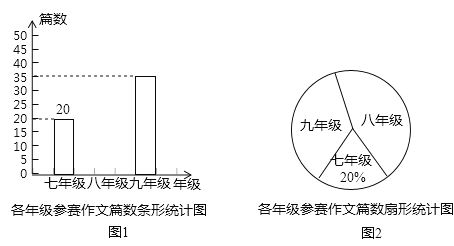
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
相关试题

