【题目】如图,小明家的住房结构平面图,(单位:米),装修房子时,他打算将卧室以外的部分都铺上地砖,
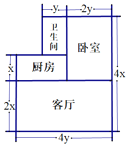
(1)若铺地砖的价格为80元/平方米,那么购买地砖需要花多少钱?(用代数式表示);
(2)已知房屋的高度为3米,现在想要在客厅和卧室的墙壁上贴上壁纸,那么需要多少平方米的壁纸(门窗所占面积忽略不计)?(用代数式表示);
(3)若x=4,y=5,且每平方米地砖的价格是90元,每平方米壁纸的价格是15元,那么,在这两项装修中,小明共要花费多少钱?(各种小的损耗不计).
参考答案:
【答案】(1)880xy
(2)![]() (平方米)
(平方米)
(3)23940(元)
【解析】
(1)求出卫生间,厨房,及客厅的面积之和即可得到需要地砖的面积; 地砖的价格为80元/平方米,求出需要的钱数即可;
(2)求出客厅与卧室的周长,乘以高,即可得到需要的壁纸数;
(3)将x=4,y=5每平方米地砖的价格是90元,每平方米壁纸的价格是15元,分别代入计算即可.
解:(1)客厅的面积是:![]() ,厨房面积是:
,厨房面积是:![]() ,卫生间的面积是:
,卫生间的面积是:![]() ,所以共需要地砖的面积为:
,所以共需要地砖的面积为:
![]() =11xy,
=11xy,
因为每平方米的价格为 80元,
故共需要80×11xy=880xy(元)
答:购买地砖需要花多少钱.
(2)根据题意得:![]() ,
,
化简得:![]()
答:需要![]() 平方米的壁纸.
平方米的壁纸.
(3)共需地砖11xy平方米,共需墙纸(![]() )平方米,将x=4,y=5代入,
)平方米,将x=4,y=5代入,
得:共需地砖:11×4×5=220(平方米),共需墙纸:24×4+36×5=276(平方米)
∵每平方米地砖的价格是90元,每平方米壁纸的价格是15元
∴共需钱数为:220×90+276×15=23940(元)
答:在这两项装修中,小明共要花费23940元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程
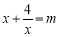 的两实根,且tan∠PCD=
的两实根,且tan∠PCD= ,求⊙O的半径.
,求⊙O的半径.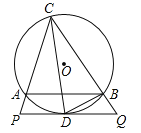
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH.
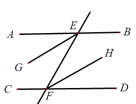
请完成以下证明过程:
证明:∵AB∥CD(已知)
∴∠AEF=∠EFD(__________________)
∵EG平分∠AEF,FH平分∠EFD(__________)
∴∠___=
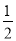 ∠AEF,∠___=
∠AEF,∠___= 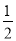 ∠EFD(____________)
∠EFD(____________)∴∠_____=∠______(等量代换)
∴EG∥FH(__________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ).

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时
 张用A方法,其余用B方法。
张用A方法,其余用B方法。(1)用
 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
相关试题

