【题目】如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a﹣40|+(b+8)2=0.点O是数轴原点.
![]()
(1)点A表示的数为 ,点B表示的数为 ,线段AB的长为 .
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为 .
(3)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?
参考答案:
【答案】(1)点A表示的数为40,点B表示的数为﹣8,线段AB的长为48;(2)8或﹣40(3)当t为4秒、10秒和14秒时,P、Q两点相距4个单位长度
【解析】
(1)根据偶次方以及绝对值的非负性即可求出a、b的值,可得点A表示的数,点B表示的数,再根据两点间的距离公式可求线段AB的长;
(2)分两种情况:点C在线段AB上,点C在射线AB上,进行讨论即可求解;
(3)分0<t≤8、8<t≤12,12<t≤48三种情况考虑,根据P,Q移动的路程结合PQ=4即可得出关于t的一元一次方程,解之即可得出结论.
解:(1)∵|a﹣40|+(b+8)2=0,
∴a﹣40=0,b+8=0,
解得a=40,b=﹣8,
AB=40﹣(﹣8)=48.
故点A表示的数为40,点B表示的数为﹣8,线段AB的长为48;
(2)点C在线段AB上,
∵AC=2BC,
∴AC=48×![]() =32,
=32,
点C在数轴上表示的数为40﹣32=8;
点C在射线AB上,
∵AC=2BC,
∴AC=40×2=80,
点C在数轴上表示的数为40﹣80=﹣40.
故点C在数轴上表示的数为8或﹣40;
(3)(i)当0<t≤8时,点Q还在点B处,
∴PQ=t=4;
(ii)当8<t≤12时,点P在点Q的右侧,
∴![]()
解得:![]() ;
;
(iii)当12<t≤48时,点P在点Q的左侧,
∴3(t﹣8)﹣t=4,
解得:t=14,
综上所述:当t为4秒、10秒和14秒时,P、Q两点相距4个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为了保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
(3)当每斤的售价定为多少元时,每天获利最大?最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
 的图像与反比例函数
的图像与反比例函数 的图像交于第一、三象限内的
的图像交于第一、三象限内的 、
、 两点,与
两点,与 轴交于点
轴交于点 ,点
,点 在
在 轴负半轴上,
轴负半轴上, ,且四边形
,且四边形 是平行四边形,点
是平行四边形,点 的纵坐标为
的纵坐标为 .
.(1)求该反比例函数和一次函数的表达式;
(2)连接
 ,求
,求 的面积;
的面积;(3)直接写出关于
 的不等式
的不等式 的解集.
的解集.
-
科目: 来源: 题型:
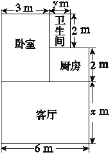
查看答案和解析>>【题目】丁丁家买了一套安置房,地面结构如图所示.
(1)写出用含x、y的式子表示地面的总面积;
(2)如果x=4 m,y=1.5 m,铺1 m2地砖的平均费用为80元,求铺地砖的总费用.
-
科目: 来源: 题型:
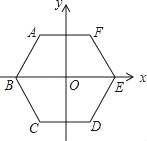
查看答案和解析>>【题目】如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2018时,顶点A的坐标为_____.
相关试题

