【题目】如图,在Rt△ABC中,∠ACB=90°,AB=10,sinA=![]() ,CD为AB边上的中线,以点B为圆心,r为半径作⊙B.如果⊙B与中线CD有且只有一个公共点,那么⊙B的半径r的取值范围为_____.
,CD为AB边上的中线,以点B为圆心,r为半径作⊙B.如果⊙B与中线CD有且只有一个公共点,那么⊙B的半径r的取值范围为_____.

参考答案:
【答案】5<r≤6或![]() .
.
【解析】分析:根据三角函数可得BC,AC,根据直角三角形斜边上的中线的性质可求CD,BD,根据三角形面积公式可求CD边的高,再根据直线与圆的位置关系即可求解.
详解:∵在Rt△ABC中,∠ACB=90°,AB=10,sinA=![]() ,
,
∴BC=6,AC=8,
∵CD为AB边上的中线,
∴CD=BD=5,
∴CD边的高=6×8÷2÷2×2÷5=![]() ,
,
∵⊙B与中线CD有且只有一个公共点,
∴⊙B的半径r的取值范围为5<r≤6或r=![]() .
.
故答案为:5<r≤6或r=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阳泉市郊区教科局提出开展“三有课堂”,某中学在一节体现“三有课堂”公开展示课上,李老师展示一幅图,条件是:C为直线AB上一点,∠DCE为直角,CF平分∠ACD,CH平分∠BCD,CG平分∠BCE,各个小组经过讨论后得到以下结论:①∠ACF与∠BCH互余 ②∠FCG与∠HCG互补 ③∠ECF与∠GCH互补 ④∠ACD﹣∠BCE=90°,聪明的你认为哪些组的结论是正确的,正确的有( )个.
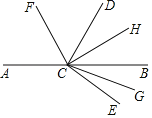
A.1B.2C.3D.4
-
科目: 来源: 题型:
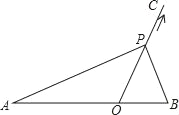
查看答案和解析>>【题目】如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.当△ABP是直角三角形时,t的值为( )
A.
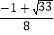 B.
B. 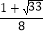 C. 1或
C. 1或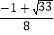 D. 1或
D. 1或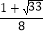
-
科目: 来源: 题型:
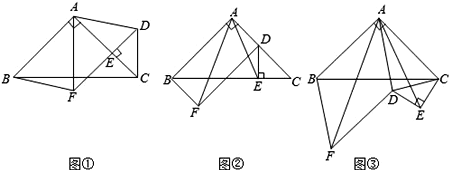
查看答案和解析>>【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在等腰△ABC中,AB=AC=
 ,BC=4,点D从A出发以每秒
,BC=4,点D从A出发以每秒 个单位的速度向点B运动,同时点E从点B出发以每秒4个单位的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F,设运动的时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为_____.
个单位的速度向点B运动,同时点E从点B出发以每秒4个单位的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F,设运动的时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为_____.
-
科目: 来源: 题型:
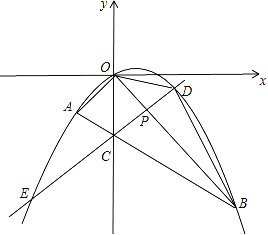
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求直线AB和OB的解析式.
(2)求抛物线的解析式.
(3)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.问△BOD的面积是否存在最大值?若存在,求出这个最大值并写出此时点D的坐标;若不存在说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为 ______________.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/4/1916730188324864/1920418179735552/STEM/955c40623e644964ae11bcb49c75f843.png]
相关试题

