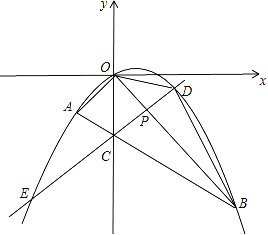
【题目】如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求直线AB和OB的解析式.
(2)求抛物线的解析式.
(3)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.问△BOD的面积是否存在最大值?若存在,求出这个最大值并写出此时点D的坐标;若不存在说明理由.
参考答案:
【答案】(1)y=![]() ,y=-x;(2)
,y=-x;(2)![]() ;(3)△BOD的面积有最大值,最大值为
;(3)△BOD的面积有最大值,最大值为![]() ,D(
,D(![]() ).
).
【解析】试题分析:(1)首先解方程得出A,B两点的坐标,利用待定系数法确定直线AB和直线OB的解析式即可;
(2)利用待定系数法求出二次函数解析式即可;
(3)利用S△BOD=S△ODQ+S△BDQ得出关于x的二次函数,进而得出最值即可.
解:(1)解方程x2-2x-3=0,
得 x1=3,x2=-1.
∵m<n,
∴m=-1,n=3,
∴A(-1,-1),B(3,-3).
设直线AB的解析式为y=kx+b
∴![]() ,
,
解得: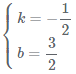 .
.
∴直线AB的解析式为y=-![]() x+
x+![]() ;
;
设直线OB的解析式为y=kx,
∴3k=-3,
解得:k=-1,
∴直线OB的解析式为y=-x;
(2)∵抛物线过原点,设抛物线的解析式为y=ax2+bx(a≠0).
∴![]() ,
,
解得: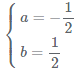 ,
,
∴抛物线的解析式为y=-![]() x2+
x2+![]() x.
x.
(3)△BOD的面积是存在最大值;
过点D作DG⊥x轴,垂足为G,交OB于Q,过B作BH⊥x轴,垂足为H.
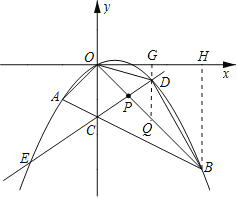
设Q(x,-x),D(x,-![]() x2+
x2+![]() x).
x).
S△BOD=S△ODQ+S△BDQ=12DQOG+12DQGH,
=![]() DQ(OG+GH),
DQ(OG+GH),
=![]() [x+(-
[x+(-![]() x2+
x2+![]() x)]×3,
x)]×3,
=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∵0<x<3,
∴当x=![]() 时,S取得最x大值为
时,S取得最x大值为![]() ,此时D(
,此时D(![]() ,-
,-![]() ).
).
-
科目: 来源: 题型:
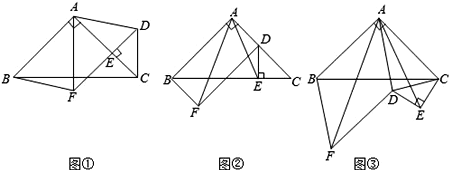
查看答案和解析>>【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AB=10,sinA=
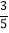 ,CD为AB边上的中线,以点B为圆心,r为半径作⊙B.如果⊙B与中线CD有且只有一个公共点,那么⊙B的半径r的取值范围为_____.
,CD为AB边上的中线,以点B为圆心,r为半径作⊙B.如果⊙B与中线CD有且只有一个公共点,那么⊙B的半径r的取值范围为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在等腰△ABC中,AB=AC=
 ,BC=4,点D从A出发以每秒
,BC=4,点D从A出发以每秒 个单位的速度向点B运动,同时点E从点B出发以每秒4个单位的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F,设运动的时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为_____.
个单位的速度向点B运动,同时点E从点B出发以每秒4个单位的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F,设运动的时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为 ______________.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/4/1916730188324864/1920418179735552/STEM/955c40623e644964ae11bcb49c75f843.png]
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高市民的精神生活美化城市环境,城市管理局从外地新进一批绿化树苗,现有两种运输方式可供选择,
方式一:使用快递公司的邮车运输,装卸收费500元,另外每公里再加收5元;
方式二:使用铁路运输公司的火车运输,装卸收费900元,另外每公里再加收3元.
(1)请分别写出邮车、火车运输的总费用为
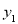 (元)、
(元)、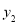 (元)与运输路程
(元)与运输路程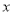 (公里)之间的函数关系式;
(公里)之间的函数关系式;(2)你认为选用哪种运输方式较好,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设
 ,
,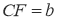 ,满足
,满足 .
.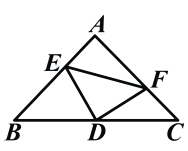
(1)求BE及CF的长。
(2)求证:
 。
。(3)在(1)的条件下,求△DEF的面积。
相关试题

