搜索
【题目】如图，Rt△ABO的顶点A是双曲线y= 
与直线y=﹣x﹣（k+1）在第二象限的交点．AB⊥x轴于B，且S△ABO= 
．
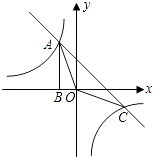
（1）求这两个函数的解析式；
（2）求直线与双曲线的两个交点A、C的坐标和△AOC的面积．
参考答案：
【答案】
（1）解：设A点坐标为（x，y），且x＜0，y＞0，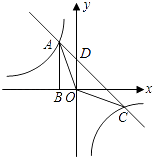 
则S△ABO= 
|BO||BA|= （﹣x）y= 
，
∴xy=﹣3，
又∵y= 
，
即xy=k，
∴k=﹣3．
∴所求的两个函数的解析式分别为y=﹣ 
，y=﹣x+2；
（2）解：由y=﹣x+2，
令x=0，得y=2．
∴直线y=﹣x+2与y轴的交点D的坐标为（0，2），
A、C两点坐标满足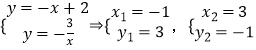 
∴交点A为（﹣1，3），C为（3，﹣1），
∴S△AOC=S△ODA+S△ODC= OD（|x1|+|x2|）= ×2×（3+1）=4．
【解析】两解析式的k一样，根据面积计算双曲线中的k较易，由公式
=2S△ABO,可求出k；（2）求交点就求两解析式联立的方程组的解，可分割△AOC为S△ODA+S△ODC，即可求出.
-
科目： 来源： 题型：
查看答案和解析>>【题目】“转化”是数学中的一种重要思想，即把陌生的问题转化成熟悉的问题，把复杂的问题转化成简单的问题，把抽象的问题转化为具体的问题．
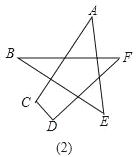
（1）请你根据已经学过的知识求出下面星形图（1）中∠A+∠B+∠C+∠D+∠E的度数；
（2）若对图（1）中星形截去一个角，如图（2），请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数；
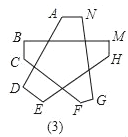
（3）若再对图（2）中的角进一步截去，你能由题（2）中所得的方法或规律，猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗？只要写出结论，不需要写出解题过程）
-
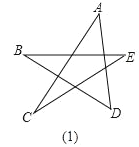
科目： 来源： 题型：
查看答案和解析>>【题目】我县盛产绿色蔬菜，生产销售一种绿色蔬菜，若在市场上直接销售，每吨利润为800元，经粗加工销售，每吨利润可达2000元，经精加工后销售，每吨利润涨至2500元．我县一家农工商公司采购这种蔬菜若干吨生产销售，若单独进行精加工，需要30天才能完成，若单独进行粗加工，需要20天才能完成．已知每天单独粗加工比单独精加工多生产10吨．
（1）试问这家农工商公司采购这种蔬菜共多少吨？
（2）由于两种加工方式不能同时进行受季节条件限制，公司必须在24天内将这批蔬菜全部销售或加工完毕，为此该公司研制了三种可行方案：
方案一：将蔬菜全部进行粗加工；
方案二：尽可能多的对蔬菜进行精加工，没有来得及进行加工的蔬菜，在市场上直接销售；
方案三：将部分蔬菜进行精加工，其余蔬菜进行粗加工，并恰好24天完成，你认为选择哪种方案获利最多？请通过计算说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制成如下统计图表(单位：cm)：
A
x<155
B
155≤x<160
C
160≤x<165
D
165≤x<170
E
x≥170
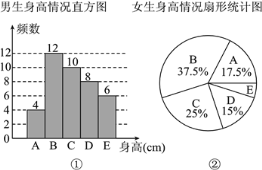
根据图表提供的信息，样本中，身高在160≤x＜170之间的女生人数为( )
A. 8 B. 6 C. 14 D. 16
-
科目： 来源： 题型：
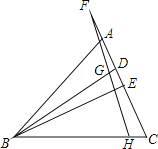
查看答案和解析>>【题目】如图，△ABC中，BD、BE分别是高和角平分线，点F在CA的延长线上，FH⊥BE，交BD于点G，交BC于点H；下列结论：①∠DBE=∠F；②2∠BEF=∠BAF+∠C；③∠F=∠BAC-∠C；④∠BGH=∠ABE+∠C，其中正确的结论有______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC中，AB=AC=4，BC=5，点D是边AB的中点，点E是边AC的中点，点P是边BC上的动点，∠DPE=∠C，则BP= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】学期结束前，学校想调查七年级学生对新课改实验教材的意见，特向七年级480名学生作了问卷调查，结果如下表所示：
意见
非常喜欢
喜欢
有一点喜欢
不喜欢
人数
240
192
44
4
（1）计算出每一种意见的人数占调查总人数的百分比；
（2）请作出反映此调查结果的扇形统计图；
（3）从统计图中你能得出什么结论？说说你的理由．
相关试题
