Question

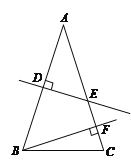
【题目】如图，已知在△ABC中，AB=AC，AB的垂直平分线DE交AC于点E，CE的垂直平分线正好经过点B，与AC相交于点F，求∠ A的度数．

Answer 1

【答案】 36°

【解析】试题分析：连接BE，根据等腰三角形的性质得出∠ABC、∠C与∠A的关系，根据DE是线段AB的中垂线得出AE=BE，∠A=∠ABE，从而根据角平分线的性质得出∠A的度数.

试题解析：连接BE ∵△ABC是等腰三角形， ∴∠ABC=∠C=①，

∵DE是线段AB的垂直平分线， ∴AE=BE， ∴∠A=∠ABE，

∵CE的垂直平分线正好经过点B，与AC相交于点可知△BCE是等腰三角形， ∴BF是∠EBC的平分线，

∴（∠ABC﹣∠A）+∠C=90°，即（∠C﹣∠A）+∠C=90°②，

①②联立得，∠A=36°． 故∠A=36°．