【题目】如图,直线L上有三个正方形a,b,c,若a,c的面积分别为1和9,则b的面积为( )

A.8 B.9 C.10 D.11
参考答案:
【答案】C
【解析】
试题分析:运用正方形边长相等,再根据同角的余角相等可得∠BAC=∠DCE,然后证明△ACB≌△DCE,再结合全等三角形的性质和勾股定理来求解即可.
解:由于a、b、c都是正方形,所以AC=CD,∠ACD=90°;

∵∠ACB+∠DCE=∠ACB+∠BAC=90°,即∠BAC=∠DCE,
在△ABC和△CED中,
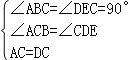 ,
,
∴△ACB≌△DCE(AAS),
∴AB=CE,BC=DE;
在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=AB2+DE2,
即Sb=Sa+Sc=1+9=10,
∴b的面积为10,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】气象台发布的卫星云图显示,代号为
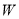 的台风在某海岛(设为点
的台风在某海岛(设为点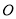 )的南偏东
)的南偏东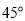 方向的
方向的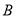 点生成,测得
点生成,测得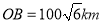 .台风中心从点
.台风中心从点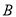 以
以 的速度向正北方向移动,经
的速度向正北方向移动,经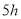 后到达海面上的点
后到达海面上的点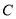 处.因受气旋影响,台风中心从点
处.因受气旋影响,台风中心从点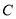 开始以
开始以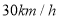 的速度向北偏西
的速度向北偏西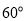 方向继续移动.以
方向继续移动.以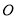 为原点建立如图所示的直角坐标系.
为原点建立如图所示的直角坐标系.(1)台风中心生成点
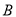 的坐标为 ,台风中心转折点
的坐标为 ,台风中心转折点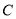 的坐标为 ;(结果保留根号)
的坐标为 ;(结果保留根号)(2)已知距台风中心
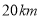 范围内均会受到台风侵袭.如果某城市(设为点
范围内均会受到台风侵袭.如果某城市(设为点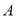 )位于点
)位于点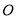 的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 分别与x轴、y轴交于
分别与x轴、y轴交于 两点,与直线
两点,与直线 交于点C(4,2).
交于点C(4,2).(1)点A坐标为( , ),B为( , );
(2)在线段
 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形 是平行四边形;
是平行四边形;(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得
 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形
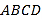 中,
中, ,
,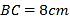 ,
,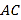 的垂直平分线
的垂直平分线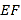 分别交
分别交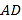 、
、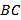 于点
于点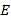 、
、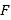 ,垂足为
,垂足为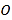 .
.(1)如图,连接
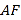 、
、 .求证四边形
.求证四边形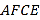 为菱形,并求
为菱形,并求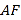 的长;
的长;(2)如图,动点
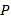 、
、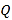 分别从
分别从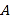 、
、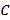 两点同时出发,沿
两点同时出发,沿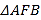 和
和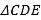 各边匀速运动一周.即点
各边匀速运动一周.即点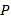 自
自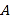 →
→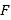 →
→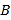 →
→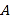 停止,点
停止,点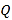 自
自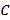 →
→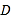 →
→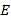 →
→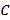 停止.在运动过程中,
停止.在运动过程中,①已知点
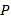 的速度为每秒5
的速度为每秒5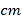 ,点
,点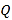 的速度为每秒4
的速度为每秒4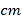 ,运动时间为
,运动时间为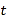 秒,当
秒,当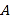 、
、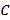 、
、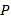 、
、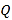 四点为顶点的四边形是平行四边形时,求
四点为顶点的四边形是平行四边形时,求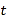 的值.
的值. ②若点
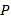 、
、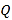 的运动路程分别为
的运动路程分别为 、
、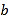 (单位:
(单位: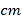 ,
,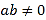 ),已知
),已知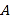 、
、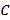 、
、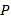 、
、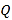 四点为顶点的四边形是平行四边形,写出
四点为顶点的四边形是平行四边形,写出 与
与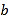 满足的数量关系式.(直接写出答案,不要求证明)
满足的数量关系式.(直接写出答案,不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
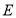 、
、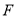 、
、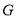 、
、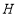 分别是四边形
分别是四边形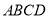 边
边 、
、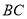 、
、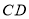 、
、 的中点,则下列说法:
的中点,则下列说法:①若
 ,则四边形
,则四边形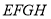 为矩形;
为矩形;②若
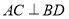 ,则四边形
,则四边形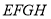 为菱形;
为菱形;③若四边形
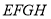 是平行四边形,则
是平行四边形,则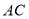 与
与 互相垂直平分;
互相垂直平分;④若四边形
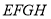 是正方形,则
是正方形,则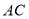 与
与 互相垂直且相等.
互相垂直且相等.其中正确的个数是( )
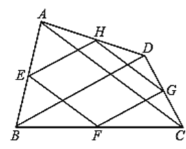
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
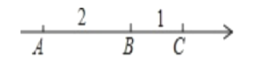
(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线过A(-1,0),B(3,0)两点,与y轴交于C点,且BC=3
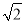 ,则这条抛物线的解析式为 ( )
,则这条抛物线的解析式为 ( )A. y=-x2+2x+3 B. y=x2-2x-3
C. y=x2+2x―3或y=-x2+2x+3 D. y=-x2+2x+3或y=x2-2x-3
相关试题

