【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O[Math Processing Error] ![]()
![]() C[Math Processing Error]
C[Math Processing Error] ![]()
![]() B[Math Processing Error]
B[Math Processing Error] ![]()
![]() A运动,点P的运动时间为t秒.
A运动,点P的运动时间为t秒.
(1)当t=5时, P点坐标为____________;
(2)当t>4时,OP+PD有最小值吗?如果有,请算出该最小值,如果没有,请说明理由;
(3)当t为何值时,△ODP是腰长为5的等腰三角形?(直接写出t的值).


参考答案:
【答案】(1)点P的坐标为(1,4);(2)有最小值,最小值为![]() ;(3)t=7或12或14.
;(3)t=7或12或14.
【解析】试题分析:
(1)由题意可知,OC=4,故当t=5时,点P在BC上,且PC=5-4=1,由此即可得此时点P的坐标;
(2)如图1,由题意可知,需分两种情况讨论,①当点P在BC上运动时,作点O关于BC的对称点O1,连接DO1,交BC于点P1,此时OP+PD最短,最短值等于DO1;②当点P在AB上运动时,当P与A重合时,OP+PD最短,此时最短值等于AO+AD;分上述两种情况计算,并比较两种情况计算结果的大小,即可得到所求值;
(3)如图2,由题意,需分OD是底边和腰两种情况讨论,①当OD是底边时,点P是OD的垂直平分线与BC的交点P1;②当OD是腰时,以D为圆心,DO为半径作圆,所作圆与BC、AB的交点即为所求P点,由图可知此时,点P有三个位置,分别在图中的P2、P3、P4处;根据四个点P的位置结合已知条件即可求出对应的t的值,并检验此时等腰△ODP的腰长是否为5即可得到答案.
试题解析:
(1)∵点C的坐标为:(0,4),
∴OC=4,
∵当t=5时,OC+CP1=5,
∴CP1=1,
∴此时点P的坐标为:P(1,4);
(2)如图1,当t>5时,点P在线段BC上或AB上,此时OP+PD有最小值,现分两种情况讨论如下:
①当点P在BC上时,
作点O关于BC为对称轴的对称点O′,此时O′(0,8),
连结O′D交BC于P,则OP+PD=O′D=![]() ;
;
②当点P在AB上时,由图可知当点P与点A重合时,OP+PD最小,此时OP+OD=OA+DA=13;
综合①②,∵![]() ,
,
∴ OP+PD的最小值是![]() ;
;

(3)如图2,由题意分OD是底边和腰两种情况讨论如下:
①当OD是底边时,点P是OD的垂直平分线与BC的交点P1,此时CP1=![]() OD=2.5,
OD=2.5,
又∵OC=4,
∴对应的t1=(OC+CP1)÷1=6.5,
∵此时△ODP的腰长=![]() ,
,
∴此种情况不符合要求;
②当OD是腰时,以D为圆心,DO为半径作圆,所作圆与BC、AB的交点P2、P3、P4为所求P点,过点P3作P3E⊥OA于点E,
由题意可知:OP2=OD=5=DP3=DP4,
∴由勾股定理可得:在Rt△OCP2中,CP2=![]() ;在Rt△DP3E中,DE=
;在Rt△DP3E中,DE=![]() ;在Rt△DP4A中,AP4=
;在Rt△DP4A中,AP4=![]() ;
;
∴t2=(OC+CP2)÷1=7;t3=(OC+CP3)÷1=12;t4=(OC+BC+AB-AP4)÷1=14;
综上所述,当t的值分别为:t=7或t=12或t=14时,△ODP是腰长为5的等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列材料:
我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等.
(1)分组分解法:将一个多项式适当分组后,可提公因式或运用公式继续分解的方法.
如:ax+by+bx+ay=(ax+bx)+(ay+by)
=x(a+b)+y(a+b)
=(a+b)(x+y)
2xy+y2﹣1+x2
=x2+2xy+y2﹣1
=(x+y)2﹣1
=(x+y+1)(x+y﹣1)
(2)拆项法:将一个多项式的某一项拆成两项后,可提公因式或运用公式继续分解的方法.如:
x2+2x﹣3
=x2+2x+1﹣4
=(x+1)2﹣22
=(x+1+2)(x+1﹣2)
=(x+3)(x﹣1)
请你仿照以上方法,探索并解决下列问题:
(1)分解因式:

(2)分解因式:x2﹣6x﹣7;
(3)分解因式:

-
科目: 来源: 题型:
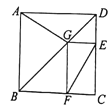
查看答案和解析>>【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A
B
载客量(人/辆)
45
30
租金(元/辆)
400
280
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆)
载客量(人)
租金(元)
A
x
45x
400x
B
5-x
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线OM⊥ON,垂足为O,三角板的直角顶点C落在∠MON的内部,三角板的另两条直角边分别与ON、OM交于点D和点B.
(1)填空:∠OBC+∠ODC= ;
(2)如图1:若DE平分∠ODC,BF平分∠CBM,求证:DE⊥BF:
(3)如图2:若BF、DG分别平分∠OBC、∠ODC的外角,判断BF与DG的位置关系,并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.

相关试题

