【题目】如图,在△ABC中,∠ACB=90°,AB=9,cosB= ![]() ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A,E之间的距离为 .
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A,E之间的距离为 . 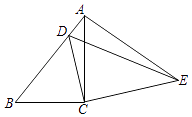
参考答案:
【答案】4 ![]()
【解析】解:∵在△ABC中,∠ACB=90°,AB=9,cosB= ![]() , ∴BC=ABcosB=9×
, ∴BC=ABcosB=9× ![]() =6,AC=
=6,AC= ![]() =3
=3 ![]() .
.
∵把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,
∴△ABC≌△EDC,BC=DC=6,AC=EC=3 ![]() ,∠BCD=∠ACE,
,∠BCD=∠ACE,
∴∠B=∠CAE.
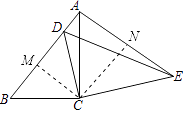
作CM⊥BD于M,作CN⊥AE于N,则∠BCM= ![]() ∠BCD,∠ACN=
∠BCD,∠ACN= ![]() ∠ACE,
∠ACE,
∴∠BCM=∠ACN.
∵在△ANC中,∠ANC=90°,AC=3 ![]() ,cos∠CAN=cosB=
,cos∠CAN=cosB= ![]() ,
,
∴AN=ACcos∠CAN=3 ![]() ×
× ![]() =2
=2 ![]() ,
,
∴AE=2AN=4 ![]() .
.
所以答案是4 ![]() .
.
【考点精析】关于本题考查的解直角三角形和旋转的性质,需要了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法);①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
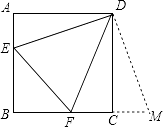
(1)求证:EF=FM.
(2)当AE=2时,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,cosA=
 ,BE,CF分别是AC,AB边上的高,联结EF,那么△AEF和△ABC的周长比为( )
,BE,CF分别是AC,AB边上的高,联结EF,那么△AEF和△ABC的周长比为( ) 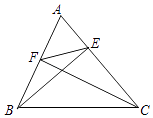
A.1:2
B.1:3
C.1:4
D.1:9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3.

(1)求EF的长;
(2)如果△BEF的面积为4,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某大型购物商场在一楼和二楼之间安装自动扶梯AC,截面如图所示,一楼和二楼地面平行(即AB所在的直线与CD平行),层高AD为8米,∠ACD=20°,为使得顾客乘坐自动扶梯时不至于碰头,A、B之间必须达到一定的距离. (参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
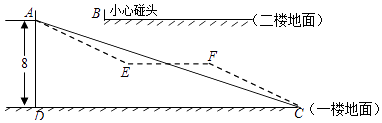
(1)要使身高2.26米的姚明乘坐自动扶梯时不碰头,那么A,B之间的距离至少要多少米?(精确到0.1米)
(2)如果自动扶梯改为由AE,EF,FC三段组成(如图中虚线所示),中间段EF为平台(即EF∥DC),AE段和FC段的坡度i=1:2,求平台EF的长度.(精确到0.1米) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CECB.
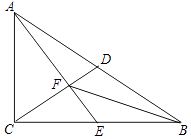
(1)求证:AE⊥CD;
(2)连接BF,如果点E是BC中点,求证:∠EBF=∠EAB.
相关试题

