【题目】如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CECB. 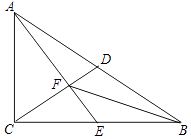
(1)求证:AE⊥CD;
(2)连接BF,如果点E是BC中点,求证:∠EBF=∠EAB.
参考答案:
【答案】
(1)证明:∵AC2=CECB,
∴ ![]() .
.
又∵∠ACB=∠ECA=90°
∴△ACB∽△ECA,
∴∠ABC=∠EAC.
∵点D是AB的中点,
∴CD=AD,
∴∠ACD=∠CAD
∵∠CAD+∠ABC=90°,
∴∠ACD+∠EAC=90°
∴∠AFC=90°,
∴AE⊥CD
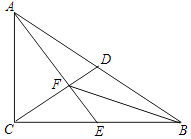
(2)证明:∵AE⊥CD,
∴∠EFC=90°,
∴∠ACE=∠EFC
又∵∠AEC=∠CEF,
∴△ECF∽△EAC
∴ ![]()
∵点E是BC的中点,
∴CE=BE,
∴ ![]()
∵∠BEF=∠AEB,
∴△BEF∽△AEB
∴∠EBF=∠EAB.
【解析】(1)先根据题意得出△ACB∽△ECA,再由直角三角形的性质得出CD=AD,由∠CAD+∠ABC=90°可得出∠ACD+∠EAC=90°,进而可得出∠AFC=90°;(2)根据AE⊥CD可得出∠EFC=90°,∠ACE=∠EFC,故可得出△ECF∽△EAC,再由点E是BC的中点可知CE=BE,故 ![]() ,根据∠BEF=∠AEB得出△BEF∽△AEB,进而可得出结论.
,根据∠BEF=∠AEB得出△BEF∽△AEB,进而可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AB=9,cosB=
 ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A,E之间的距离为 .
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A,E之间的距离为 . 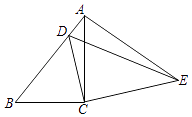
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3.

(1)求EF的长;
(2)如果△BEF的面积为4,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某大型购物商场在一楼和二楼之间安装自动扶梯AC,截面如图所示,一楼和二楼地面平行(即AB所在的直线与CD平行),层高AD为8米,∠ACD=20°,为使得顾客乘坐自动扶梯时不至于碰头,A、B之间必须达到一定的距离. (参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
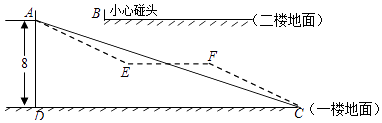
(1)要使身高2.26米的姚明乘坐自动扶梯时不碰头,那么A,B之间的距离至少要多少米?(精确到0.1米)
(2)如果自动扶梯改为由AE,EF,FC三段组成(如图中虚线所示),中间段EF为平台(即EF∥DC),AE段和FC段的坡度i=1:2,求平台EF的长度.(精确到0.1米) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c过点B(3,0),C(0,3),D为抛物线的顶点.
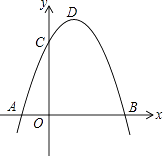
(1)求抛物线的解析式以及顶点坐标;
(2)点C关于抛物线y=﹣x2+bx+c对称轴的对称点为E点,联结BC,BE,求∠CBE的正切值;
(3)点M是抛物线对称轴上一点,且△DMB和△BCE相似,求点M坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是矩形,cot∠ADB=
 ,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.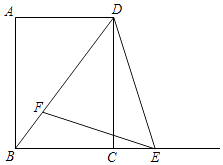
(1)求线段BD的长;
(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;
(3)当△DEF为等腰三角形时,求线段BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,AB=5,联结BD,sin∠ABD=
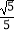 .点P是射线BC上的一个动点(点P不与点B重合),联结AP,与对角线BD相交于点E,联结EC.
.点P是射线BC上的一个动点(点P不与点B重合),联结AP,与对角线BD相交于点E,联结EC.
(1)求证:AE=CE;
(2)当点P在线段BC上时,设BP=x,△PEC的面积为y,求y关于x的函数解析式,并写出它的定义域;
(3)当点P在线段BC的延长线上时,若△PEC是直角三角形,求线段BP的长.
相关试题

