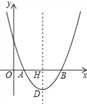
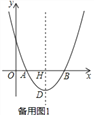
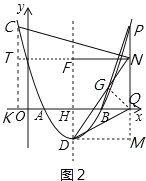
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣10ax+16a(a≠0)交x轴于A、B两点,抛物线的顶点为D,对称轴与x轴交于点H,且AB=2DH.
(1)求a的值;
(2)点P是对称轴右侧抛物线上的点,连接PD,PQ⊥x轴于点Q,点N是线段PQ上的点,过点N作NF⊥DH于点F,NE⊥PD交直线DH于点E,求线段EF的长;
(3)在(2)的条件下,连接DN、DQ、PB,当DN=2QN(NQ>3),2∠NDQ+∠DNQ=90°时,作NC⊥PB交对称轴左侧的抛物线于点C,求点C的坐标.
参考答案:
【答案】(1)![]() ;(2)3;(3)点C(﹣1,9)..
;(2)3;(3)点C(﹣1,9)..
【解析】试题分析:(1)根据y=ax2-10ax+16a可以求得当y=0时,x的值,从而可以求得点A、B的坐标,由抛物线的顶点为D,对称轴与x轴交于点H,且AB=2DH,从而可以求得a的值;
(2)根据已知条件作出相应的图形,然后根据题意题目中的数量关系,通过灵活变形可以求得EF的长;
(3)根据题意可以画出相应的图形,然后根据题目中的关系,利用三角形相似,灵活变化可以求得点C的坐标.
试题解析:(1)令y=0,得x=2或x=8,∴点A(2,0),B(8,0),∴AB=6,
∵AB=2DH,∴DH=3,
∵OH=2+![]() ,∴D(5,﹣3),∴﹣3=a×52﹣10a×5+16a,得a=
,∴D(5,﹣3),∴﹣3=a×52﹣10a×5+16a,得a=![]() ;
;
(2)如图1,过点D作PQ的垂线,交PQ的延长线于点M,
∵NE⊥PD,∴∠DPN+∠PNE=90°,∵NF⊥DE,∴∠FEN+∠FNE=90°,
又∵DH⊥x轴,PQ⊥x轴,∴DE∥PQ,∴∠FEN=∠PNE,∴∠DPM=∠ENF,∴△EFN∽△DMP,
∴![]() ,设点P(t,
,设点P(t, ![]() ),则FN=DM=t﹣5,PM=
),则FN=DM=t﹣5,PM=![]() +3,代入解得EF=3;
+3,代入解得EF=3;
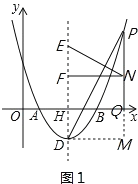
(3)如图2,作QG⊥DN于点G,∵DF∥PQ,∴∠FDN=∠DNQ,∵2∠NDQ+∠DNQ=90°,
∴2∠NDQ+∠FDN=90°,∵∠FDM=90°,∴∠NDM=2∠NDQ,∴∠NDQ=∠MDQ,∴QG=QM=DH=3,
设QN=m,则DN=2m,∵sin∠DNM=![]() ,sin∠QNG=
,sin∠QNG=![]() ,sin∠DNM=sin∠QNG,
,sin∠DNM=sin∠QNG,
∴![]() ,得DM=6=DG,∴OQ=5+6=11,
,得DM=6=DG,∴OQ=5+6=11,
∴点P的纵坐标是: ![]() =9,∴点P(11,9),
=9,∴点P(11,9),
∵NG=2m﹣6,在Rt△NGQ中,QG2+NG2=QN2,
∴32+(2m﹣6)2=m2,得,m=3(舍)或m=5,
设C(n, ![]() ),作CK⊥x轴于点K,作NF⊥CK于点K,则CT=
),作CK⊥x轴于点K,作NF⊥CK于点K,则CT=![]() ,NT=11﹣n,
,NT=11﹣n,
∵P(11,9),则BQ=11﹣8=3,PQ=9,
∵CN⊥PB,PQ∥CK,PQ⊥x轴, ∴△CTN∽△BQP,
∴![]() , 即
, 即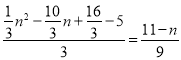 , 解得,n=﹣1或n=10(舍去),
, 解得,n=﹣1或n=10(舍去),
∴点C(﹣1,9).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场投入
 元资金购进甲、乙两种矿泉水共
元资金购进甲、乙两种矿泉水共 箱,矿泉水的成本价和销售价如表所示:
箱,矿泉水的成本价和销售价如表所示:(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完
 箱矿泉水,该商场共获得利润多少元?
箱矿泉水,该商场共获得利润多少元?类别
成本价(元/箱)
销售价(元/箱)
甲


乙


-
科目: 来源: 题型:
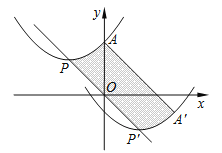
查看答案和解析>>【题目】如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,安全快捷、平稳舒适的中国高铁,为世界高速铁路商业运营树立了新的标杆.随着中国特色社会主义进入新时代,作为“中国名片”的高速铁路也将踏上自己的新征程,跑出发展新速度,这就意味着今后外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从A地到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:
(1)普通列车的行驶路程为多少千米?
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B两点在数轴上,点A表示的数为–10,OB=4OA,点M以每秒2个单位长度的速度从点A开始向左运动,点N以每秒3个单位长度的速度从点B开始向左运动(点M和点N同时出发).

(1)数轴上点B对应的数是__________,线段AB的中点C对应的数是__________;
(2)经过几秒,点M、点N到原点的距离相等?
-
科目: 来源: 题型:
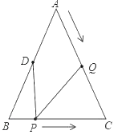
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点,如果点P在线段BC上以2cm/s的速度由点B向点C运动,同时,点Q在线段AC上由点A向点C 以4cm/s的速度运动.若点P、Q两点分别从点B、A同时出发.
(1)经过2秒后,求证:∠DPQ=∠C.
(2)若△CPQ的周长为18cm,问经过几秒钟后,△CPQ是等腰三角形?
相关试题

