【题目】
(1)如果点P到点A,点B的距离相等,那么x=______;
(2)当x=______时,点P到点A,点B的距离之和是6;
(3)若点P到点A,点B的距离之和最小,则x的取值范围是______;
(4)在数轴上,点M,N表示的数分别为x![]() ,x
,x![]() ,我们把x
,我们把x![]() ,x
,x![]() 之差的绝对值叫做点M,N之间的距离,即MN="|" x
之差的绝对值叫做点M,N之间的距离,即MN="|" x![]() -x
-x![]() |.若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动______秒时,点P到点E,点F的距离相等.
|.若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动______秒时,点P到点E,点F的距离相等.
参考答案:
【答案】(1)-1;(2)-4或2;(3)![]() ;(4)
;(4)![]() 或2.
或2.
【解析】试题分析:(1)根据题意列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值;
的值;
根据题意列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值;
的值;
(3)点P到点A,点B的距离之和最小,则点P在线段AB上,求出![]() 的取值范围即可;
的取值范围即可;
(4)设![]() 秒时点P到点E,点F的距离相等,根据题意列出关于
秒时点P到点E,点F的距离相等,根据题意列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值.
的值.
试题解析:(1)根据题意得,![]()
![]()
根据题意得,![]() 解得
解得![]() 或
或![]() ;
;
点P到点A,点B的距离之和最小,点P在线段AB上,则![]() 的取值范围为
的取值范围为![]() ;
;
设![]() 秒时点P到点E,点F的距离相等,根据题意得:
秒时点P到点E,点F的距离相等,根据题意得:![]() 解得:
解得:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,点E是平面内异于点A的任意一点,以线
段AE为边作正方形AEFG,连接EB,GD.
(1) 如图1,判断EB与GD的关系并说明理由;
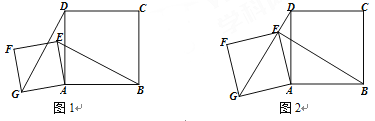
(2) 如图2,若点E在线段DG上,AB=5,AG=3
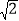 ,求BE的长.
,求BE的长. -
科目: 来源: 题型:
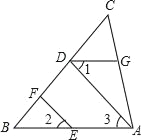
查看答案和解析>>【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵ ,(已知)
∴∠AGD= (等式性质)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=
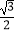 ,则∠CDE+∠ACD=( )
,则∠CDE+∠ACD=( ) 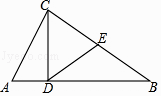
A.60°
B.75°
C.90°
D.105° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是二次函数y=ax2+bx+c的图象,对下列结论①ab>0,②abc>0,③
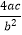 <1,其中错误的个数是( )
<1,其中错误的个数是( ) 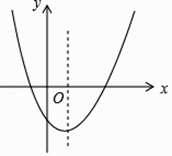
A.3
B.2
C.1
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上,点 A 的初始位置表示的数为 1,现点 A 做如下移动:第 1 次点 A 向左移动 3 个单位长度至点 A1,第 2 次从点 A1 向右移动 6 个单位长度至点 A2,第 3 次从点 A2 向左移动 9 个单位长度至点 A3,…,按照这种移动方式进行下去,点 A4 表示的数,是__________ ,如果点 An 与原点的距离不小于 20, 那么 n 的最小值是________________ .
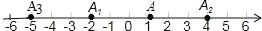
-
科目: 来源: 题型:
查看答案和解析>>【题目】实践操作
如图1,在矩形纸片ABCD中,AB>AD.
第一步:如图2,将图1中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图4,将图3中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.

问题解决
(1) 如图2,说明四边形AEFD是正方形;
(2) 如图4,判断NF与ND′的数量关系,并说明理由;
探索发现
(3)图4中MH与AM之间满足MH=nAM,请求出n的值.
相关试题

