【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务. 已知每台GH型产品由4个G型装置和3个H型装置配套组成. 工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G 型装置的加工,且每人每天只能加工4个G型装置. 请问至少需要补充多少名新工人?
参考答案:
【答案】(1)每天能组装48套GH型电子产品;(2)至少应招聘30名新工人.
【解析】
试题分析:(1)设有x名工人加工G型装置,则有(80-x)名工人加工H型装置,利用每台GH型产品由4个G型装置和3个H型装置配套组成得出等式求出答案;
(2)设招聘a名新工人加工G型装置,设x名工人加工G型装置,(80-x)名工人加工H型装置,进而利用每天加工的G、H型装置数量正好全部配套组成GH型产品得出等式表示出x的值,进而利用不等式解法得出答案.
试题解析:(1)设有x名工人加工G型装置,
则有(80-x)名工人加工H型装置,
根据题意,
![]() ,
,
解得x=32,
则80-32=48(套),
答:每天能组装48套GH型电子产品;
(2)设招聘a名新工人加工G型装置
仍设x名工人加工G型装置,(80-x)名工人加工H型装置,
根据题意,
![]() ,
,
整理可得,x=![]() ,
,
另外,注意到80-x≥![]() ,即x≤20,
,即x≤20,
于是![]() ≤20,
≤20,
解得:a≥30,
答:至少应招聘30名新工人,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图坐标系中,O(0,0) ,A(6,6
 ),B(12,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(12,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE= ,则CE : DE的值是______.
,则CE : DE的值是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
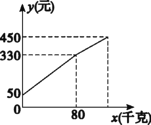
(1)农民自带的零钱是多少?
(2)降价前每千克西瓜出售的价格是多少?
(3)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?
(4)请问这个水果贩子一共赚了多少钱?
-
科目: 来源: 题型:
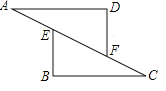
查看答案和解析>>【题目】在△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:(1)AD=CB;(2)AE=CF;(3)∠B=∠D;(4)AD∥BC.请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,求两次都摸到红球的概率.(请用“画树状图”或“列表”等方式给出分析过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.

(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知4×16m×64m=421,求m的值.
相关试题

