【题目】甲、乙两人参加学校组织的理化实验操作测试,近期的5次测试成绩如图所示.

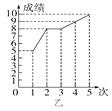
(1)请你根据图中的数据填写表格;
姓名 | 平均数 | 众数 | 方差 |
甲 | 8 | ||
乙 | 8 | 2.8 |
(2)从平均数和方差相结合看,谁的成绩好些?从发展趋势来看,谁的成绩好些?
参考答案:
【答案】(1)8 0.4 8;(2)从平均数和方差相结合看,甲的成绩好些;从发展趋势来看,乙的成绩好些.
【解析】(1)直接结合图中数据结合平均数以及方差求法分别得出答案;
(2)利用方差反映数据稳定性平均数是反映整体的平均水平进而分析得出答案.
(1)如图所示:乙的平均数为:![]()
S2甲=![]()
=0.4;
由图中数据可得:甲组数据的众数为8,
姓名 | 平均数 | 众数 | 方差 |
甲 | 8 | 8 | 0.4 |
乙 | 8 | 8 | 2.8 |
(2)从平均数和方差相结合看,甲的成绩好些;
从发展趋势来看,乙的成绩好些.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家5月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某单元楼居民六月份的用电(单位:度)情况,则关于用电量描述不正确的是( )
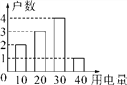
A. 众数为30 B. 中位数为30 C. 平均数为24 D. 方差为84
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是某城市四月份1至8日的日最高气温随时间变化的折线统计图,小刚根据图1将数据统计整理后制成了图2.
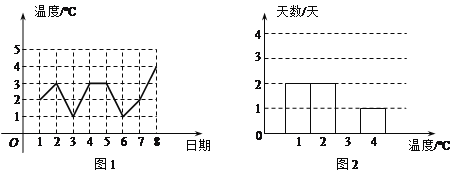
根据图中信息,解答下列问题:
(1)将图2补充完整;
(2)这8天的日最高气温的中位数是 C;
(3)计算这8天的日最高气温的平均数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有A,B两点,所表示的有理数分别为a、b,已知AB=12,原点O是线段AB上的一点,且OA=2OB.
(1)a= ,b= .
(2)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,设运动时间为t秒,当点P与点Q重合时,P,Q两点停止运动.
①当t为何值时,2OP﹣OQ=4;
②当点P到达点O时,动点M从点O出发,以每秒3个单位长度的速度也向右运动,当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后再立即返回,以同样的速度向点Q运动,如此往返,直到点P,Q停止时,点M也停止运动,求在此过程中点M行驶的总路程,并直接写出点M最后位置在数轴上所对应的有理数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( ) ①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.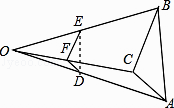
A.1
B.2
C.3
D.4
相关试题

