【题目】如图,数轴上有A,B两点,所表示的有理数分别为a、b,已知AB=12,原点O是线段AB上的一点,且OA=2OB.
(1)a= ,b= .
(2)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,设运动时间为t秒,当点P与点Q重合时,P,Q两点停止运动.
①当t为何值时,2OP﹣OQ=4;
②当点P到达点O时,动点M从点O出发,以每秒3个单位长度的速度也向右运动,当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后再立即返回,以同样的速度向点Q运动,如此往返,直到点P,Q停止时,点M也停止运动,求在此过程中点M行驶的总路程,并直接写出点M最后位置在数轴上所对应的有理数.
![]()
参考答案:
【答案】(1)﹣8;4;(2)①t为1.6秒或8秒时,2OP﹣OQ=4;②点M行驶的总路程为24和点M最后位置在数轴上对应的实数为16.
【解析】
(1)由AO=2OB可知,将12平均分为3份,其中AO占两份为8,BO占一份为4,同时注意A点在原点左侧,B点在原点右侧;
(2)①先确定停止运动的时间,再分点P在原点左侧和右侧两种情况讨论;②点M运动的时间就是点P从点O开始到追到点Q的时间,设点M运动的时间为t秒,列式2t-t=8求解即可.
(1)∵AB=12,AO=2OB,
∴AO=8,OB=4,
∴A点所表示的实数为﹣8,B点所表示的实数为4,
∴a=﹣8,b=4.
故答案是:﹣8;4;
(2)①当点P与点Q重合时,如图,
![]()
2t=12+t,t=12,
则,当0<t<4时,如图,
![]()
AP=2t,OP=8﹣2t,BQ=t,OQ=4+t,
∵2OP﹣OQ=4,
∴2(8﹣2t)﹣(4+t)=4,
t=![]() =1.6,
=1.6,
当4<t<12时,如图,
![]()
OP=2t﹣8,OQ=4+t,
则2(2t﹣8)﹣(4+t)=4,解得t=8,
综上所述,当t为1.6秒或8秒时,2OP﹣OQ=4;
②当点P到达点O时,8÷2=4,此时,OQ=4+t=8,即点Q所表示的实数为8,如图,
![]()
设点M运动的时间为t秒,
由题意得:2t﹣t=8,解得t=8,
此时,点P表示的实数为8×2=16,所以点M表示的实数也是16,
∴点M行驶的总路程为:3×8=24,
答:点M行驶的总路程为24和点M最后位置在数轴上对应的实数为16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是某城市四月份1至8日的日最高气温随时间变化的折线统计图,小刚根据图1将数据统计整理后制成了图2.
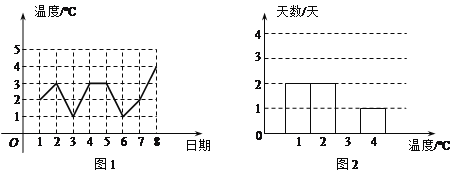
根据图中信息,解答下列问题:
(1)将图2补充完整;
(2)这8天的日最高气温的中位数是 C;
(3)计算这8天的日最高气温的平均数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人参加学校组织的理化实验操作测试,近期的5次测试成绩如图所示.

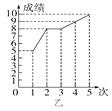
(1)请你根据图中的数据填写表格;
姓名
平均数
众数
方差
甲
8
乙
8
2.8
(2)从平均数和方差相结合看,谁的成绩好些?从发展趋势来看,谁的成绩好些?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( ) ①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.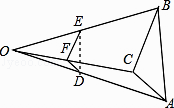
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[
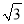 ]=1.现对72进行如下操作:72
]=1.现对72进行如下操作:72 [
[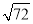 ]=8
]=8 [
[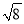 ]=2
]=2 [
[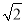 ]=1,这样对72进行3次操作后变为1,类似地,①对81进行________次操作后变为1;②进行3次操作后变为1的所有正整数中,最大的是________.
]=1,这样对72进行3次操作后变为1,类似地,①对81进行________次操作后变为1;②进行3次操作后变为1的所有正整数中,最大的是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】设边长为3的正方形的对角线长为a.下列关于a的四种说法: ①a是无理数;
②a可以用数轴上的一个点来表示;
③3<a<4;
④a是18的算术平方根.
其中,所有正确说法的序号是( )
A.①④
B.②③
C.①②④
D.①③④
相关试题

