【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:

(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
参考答案:
【答案】(1)y与x之间的函数表达式是y=-2x+200;(2)W与x之间的函数表达式是W=-2x2+280x-8000;(3)当40≤x≤70时,W随x的增大而增大,当70≤x≤80时,W随x的增大而减小,售价为70元时获得最大利润,最大利润是1800元.
【解析】试题分析:(1)用待定系数法求一次函数的表达式;(2)利用利润的定义,求![]() 与
与![]() 之间的函数表达式;(3)利用二次函数的性质求极值.
之间的函数表达式;(3)利用二次函数的性质求极值.
试题解析:解:(1)设![]() ,由题意,得
,由题意,得![]() ,解得
,解得![]() ,∴所求函数表达式为
,∴所求函数表达式为![]() .
.
(2)![]() .
.
(3)![]() ,其中
,其中![]() ,∵
,∵![]() ,
,
∴当![]() 时,
时,![]() 随
随![]() 的增大而增大,当
的增大而增大,当![]() 时,
时,![]() 随
随![]() 的增大而减小,当售价为70元时,获得最大利润,这时最大利润为1800元.
的增大而减小,当售价为70元时,获得最大利润,这时最大利润为1800元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,AB=1,则EF的长是( )
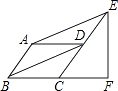
A.1.5
B.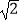
C.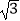
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形
 ,点
,点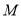 为边
为边 的中点.
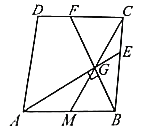
的中点.(1)如图1,点
 为线段
为线段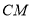 上的一点,且
上的一点,且 ,延长
,延长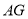 ,
,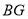 分别与边
分别与边 ,
,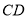 交于点
交于点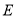 ,
, .
.
①求证:
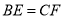 ;
;②求证:
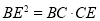 .
.(2)如图2,在边
 上取一点
上取一点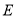 ,满足
,满足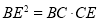 ,连接
,连接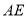 交
交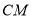 于点
于点 ,连接
,连接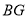 延长交
延长交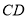 于点
于点 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列句子中,不是命题的是( )
A.三角形的内角和等于180度
B.对顶角相等
C.过一点作已知直线的垂线
D.两点确定一条直线. -
科目: 来源: 题型:
查看答案和解析>>【题目】在可以不同年的条件下,下列结论叙述正确的是( )
A.400个人中至少有两人生日相同
B.300个人至少有两人生日相同
C.300个人一定没有两人生日相同
D.300个人一定有两人生日相同 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形两边的长分别为1、5,第三边长为整数,则第三边的长为_____.
相关试题

